• 17 can be written using four 4's:
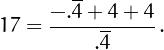
• McGuire, Tugemann & Civario proved in 2012 that 17 is the minimum possible number of givens for a Sudoku puzzle with unique solution.
• G. Szekeres & L. Peters proved that given 17 points in general position, there are always six of them at the corners of a convex hexagon.
17 has 2 divisors, whose sum is σ = 18. Its totient is φ = 16.
The previous prime is 13. The next prime is 19. The reversal of 17 is 71.
17 is nontrivially palindromic in base 2, base 4 and base 16.
It is a Cunningham number, because it is equal to 24+1.
17 is an esthetic number in base 4, base 5, base 7, base 8 and base 15, because in such bases its adjacent digits differ by 1.
It is a strong prime.
It can be written as a sum of positive squares in only one way, i.e., 16 + 1 = 4^2 + 1^2 .
17 is a truncatable prime.
It is an emirp because it is prime and its reverse (71) is a distict prime.
It is a cyclic number.
It is not a de Polignac number, because 17 - 22 = 13 is a prime.
Together with 19, it forms a pair of twin primes.
It is a Chen prime.
It is a Leyland number of the form 32 + 23.
It is a hungry number.
17 is an undulating number in base 4.
It is the 10-th Perrin number.
17 is a nontrivial repdigit in base 16.
It is a plaindrome in base 3, base 6, base 7, base 9, base 10, base 11, base 12, base 13, base 14, base 15 and base 16.
It is a nialpdrome in base 5, base 8 and base 16.
It is a zygodrome in base 16.
Being equal to 2×32-1, it is a generalized Woodall number.
It is a pernicious number, because its binary representation contains a prime number (2) of ones.
It is a good prime.
It is a Pierpont prime, being equal to 24 ⋅ 30 + 1.
A polygon with 17 sides can be constructed with ruler and compass.
It is a polite number, since it can be written as a sum of consecutive naturals, namely, 8 + 9.
It is an arithmetic number, because the mean of its divisors is an integer number (9).
It is a Proth number, since it is equal to 1 ⋅ 24 + 1 and 1 < 24.
It is an amenable number.
17 is a deficient number, since it is larger than the sum of its proper divisors (1).
17 is an equidigital number, since it uses as much as digits as its factorization.
17 is an evil number, because the sum of its binary digits is even.
The product of its digits is 7, while the sum is 8.
The square root of 17 is about 4.1231056256. The cubic root of 17 is about 2.5712815907.
Adding to 17 its reverse (71), we get a palindrome (88).
The spelling of 17 in words is "seventeen", and thus it is an aban number, an iban number, an oban number, and an uban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.077 sec. • engine limits •

