• 696 can be written using four 4's:
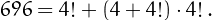
696 has 16 divisors (see below), whose sum is σ = 1800. Its totient is φ = 224.
The previous prime is 691. The next prime is 701.
696 is nontrivially palindromic in base 10.
696 is digitally balanced in base 2, because in such base it contains all the possibile digits an equal number of times.
It is an interprime number because it is at equal distance from previous prime (691) and next prime (701).
It is an alternating number because its digits alternate between even and odd.
696 is an undulating number in base 10.
It is a plaindrome in base 14.
It is a nialpdrome in base 9.
It is a congruent number.
It is not an unprimeable number, because it can be changed into a prime (691) by changing a digit.
It is a pernicious number, because its binary representation contains a prime number (5) of ones.
It is a polite number, since it can be written in 3 ways as a sum of consecutive naturals, for example, 10 + ... + 38.
It is an amenable number.
It is a practical number, because each smaller number is the sum of distinct divisors of 696, and also a Zumkeller number, because its divisors can be partitioned in two sets with the same sum (900).
696 is an abundant number, since it is smaller than the sum of its proper divisors (1104).
It is a pseudoperfect number, because it is the sum of a subset of its proper divisors.
696 is a wasteful number, since it uses less digits than its factorization.
696 is an odious number, because the sum of its binary digits is odd.
The sum of its prime factors is 38 (or 34 counting only the distinct ones).
The product of its digits is 324, while the sum is 21.
The square root of 696 is about 26.3818119165. The cubic root of 696 is about 8.8620952434.
Adding to 696 its sum of digits (21), we get a palindrome (717).
It can be divided in two parts, 69 and 6, that multiplied together give a palindrome (414).
The spelling of 696 in words is "six hundred ninety-six", and thus it is an aban number and an oban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.042 sec. • engine limits •

