The first 600 Moran numbers :
18, 21, 27, 42, 45, 63, 84, 111, 114, 117, 133, 152, 153, 156, 171, 190, 195, 198, 201, 207, 209, 222, 228, 247, 261, 266, 285, 333, 370, 372, 399, 402, 407, 423, 444, 465, 481, 511, 516, 518, 531, 555, 558, 592, 603, 629, 645, 666, 711, 730, 732, 738, 774, 777, 801, 803, 804, 846, 888, 915, 954, 999, 1011, 1016, 1017, 1090, 1095, 1098, 1101, 1141, 1143, 1164, 1168, 1185, 1233, 1236, 1251, 1270, 1278, 1304, 1308, 1341, 1387, 1413, 1417, 1455, 1494, 1503, 1524, 1526, 1545, 1611, 1630, 1635, 1651, 1659, 1679, 1744, 1746, 1810, 1812, 1818, 1853, 1854, 1896, 1898, 1905, 1926, 1962, 2007, 2022, 2043, 2061, 2085, 2119, 2151, 2159, 2172, 2202, 2265, 2282, 2286, 2289, 2313, 2316, 2353, 2355, 2358, 2398, 2421, 2445, 2466, 2532, 2534, 2608, 2667, 2682, 2710, 2715, 2718, 2771, 2794, 2826, 2889, 2919, 2934, 3031, 3032, 3033, 3070, 3077, 3097, 3123, 3141, 3165, 3184, 3231, 3252, 3258, 3297, 3303, 3324, 3345, 3383, 3411, 3435, 3438, 3439, 3474, 3501, 3523, 3546, 3582, 3586, 3615, 3699, 3749, 3768, 3781, 3980, 3982, 4041, 4044, 4065, 4086, 4113, 4155, 4179, 4194, 4203, 4245, 4311, 4330, 4336, 4338, 4378, 4404, 4518, 4577, 4605, 4607, 4626, 4683, 4734, 4776, 4809, 4842, 4887, 4912, 4975, 5013, 5052, 5055, 5058, 5094, 5121, 5149, 5161, 5219, 5230, 5235, 5274, 5306, 5410, 5496, 5505, 5526, 5634, 5691, 5697, 5706, 5784, 5817, 5833, 5943, 5962, 6062, 6064, 6066, 6130, 6135, 6246, 6282, 6310, 6315, 6331, 6352, 6354, 6443, 6447, 6462, 6573, 6606, 6648, 6714, 6754, 6775, 6777, 6792, 6822, 6939, 6951, 7033, 7077, 7146, 7212, 7218, 7305, 7322, 7329, 7361, 7362, 7368, 7479, 7501, 7542, 7543, 7580, 7587, 7588, 7675, 7707, 7833, 7859, 7902, 7940, 7944, 7982, 8082, 8088, 8110, 8115, 8203, 8205, 8226, 8227, 8289, 8334, 8337, 8338, 8376, 8397, 8406, 8559, 8596, 8622, 8660, 8717, 8734, 8808, 8841, 8937, 8952, 9012, 9015, 9054, 9093, 9096, 9099, 9105, 9162, 9219, 9232, 9253, 9369, 9414, 9475, 9526, 9528, 9693, 9723, 9740, 9816, 9854, 9909, 9925, 10012, 10014, 10053, 10090, 10095, 10096, 10107, 10109, 10161, 10213, 10232, 10236, 10278, 10279, 10307, 10308, 10346, 10365, 10386, 10479, 10524, 10543, 10566, 10630, 10635, 10674, 10727, 10782, 10818, 10901, 10905, 10926, 10963, 10968, 10983, 11007, 11028, 11061, 11085, 11133, 11170, 11202, 11241, 11244, 11265, 11331, 11354, 11355, 11358, 11487, 11511, 11530, 11535, 11538, 11574, 11601, 11604, 11606, 11646, 11647, 11688, 11710, 11754, 11805, 11824, 11862, 11976, 11991, 12102, 12108, 12165, 12181, 12186, 12252, 12294, 12303, 12345, 12362, 12435, 12438, 12563, 12612, 12618, 12694, 12747, 12762, 12873, 12942, 12984, 13023, 13044, 13086, 13111, 13116, 13117, 13118, 13131, 13155, 13194, 13245, 13264, 13374, 13401, 13404, 13486, 13518, 13598, 13605, 13626, 13842, 13848, 13881, 13882, 13914, 14031, 14052, 14055, 14093, 14099, 14103, 14126, 14128, 14166, 14211, 14230, 14346, 14383, 14412, 14505, 14521, 14562, 14568, 14704, 14769, 14780, 14814, 14856, 14922, 15001, 15003, 15021, 15135, 15223, 15267, 15310, 15315, 15354, 15393, 15409, 15426, 15462, 15519, 15534, 15579, 15623, 15689, 15751, 15771, 15775, 15849, 15864, 15938, 16035, 16101, 16142, 16144, 16149, 16210, 16258, 16305, 16326, 16389, 16527, 16542, 16580, 16584, 16654, 16659, 16722, 17001, 17008, 17046, 17153, 17154, 17283, 17406, 17409, 17448, 17461, 17469, 17592, 17660, 17668, 17736, 17777, 17793, 17803, 17842, 17847, 17887, 17913, 18010, 18015, 18039, 18071, 18162, 18168, 18234, 18238, 18279, 18299, 18342, 18380, 18417, 18456, 18475, 18543, 18653, 18657, 18702, 18740, 18925, 18927, 19047, 19067, 19134, 19171, 19242, 19426, 19464, 19601, 19629, 19682, 19752, 19791, 19820, 19953, 20024, 20028, 20133, 20137, 20151, 20170, 20197, 20312, 20316, 20371, 20403, 20421, 20426, 20464, 20530, 20603, 20715, 20718, 20752, 20754, 20934, 20937, 21036, 21051, 21073, 21078, 21102.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 642344 values, from 18 to 99999965).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 327879 | 314465 | 2 | ||||||||
| 3 | 430067 | 102147 | 110130 | 3 | |||||||
| 4 | 175995 | 159091 | 151884 | 155374 | 4 | ||||||
| 5 | 138022 | 136059 | 124212 | 128641 | 115410 | 5 | |||||
| 6 | 222334 | 52506 | 55904 | 207733 | 49641 | 54226 | 6 | ||||
| 7 | 75719 | 94216 | 94322 | 94721 | 94409 | 94816 | 94141 | 7 | |||
| 8 | 56452 | 80472 | 75765 | 78538 | 119543 | 78619 | 76119 | 76836 | 8 | ||
| 9 | 212296 | 35536 | 39953 | 118485 | 32432 | 33121 | 99286 | 34179 | 37056 | 9 | |
| 10 | 70306 | 74030 | 68788 | 67035 | 65150 | 67716 | 62029 | 55424 | 61606 | 50260 | 10 |
| 11 | 55273 | 58857 | 58608 | 59073 | 58256 | 59347 | 57800 | 59203 | 57896 | 59252 | 58779 |
A pictorial representation of the table above
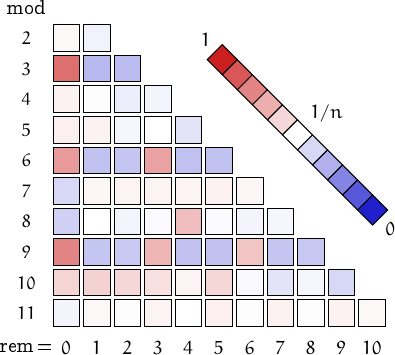
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits