A number 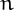 is said to be perfect if
is said to be perfect if 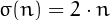 , i.e., if the sum of the proper divisors of
, i.e., if the sum of the proper divisors of 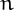 is equal to
is equal to 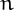 .
.
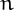 is said to be perfect if
is said to be perfect if 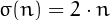 , i.e., if the sum of the proper divisors of
, i.e., if the sum of the proper divisors of 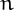 is equal to
is equal to 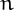 .
.
For example, 28 is perfect since 1 + 2 + 4 + 7 + 14 = 28.
It was known to Euclid that if 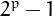 is prime, then
is prime, then 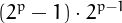 is a perfect number. Much time later, Euler proved that all the even perfect numbers are of this form, but it is not know if there are infinite such numbers.
is a perfect number. Much time later, Euler proved that all the even perfect numbers are of this form, but it is not know if there are infinite such numbers.
It is not known if an odd perfect number may exist. However, Ochem & Rao have recently proved that such a number, if exists, must be greater than 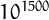 .
.
The sum of the reciprocals of the divisors of a perfect number is always equal to 2.
It is easy to see that every even perfect number is also a triangular and a hexagonal number.
The first perfect numbers are 6, 28, 496, 8128, 33550336, 8589869056, 137438691328.
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
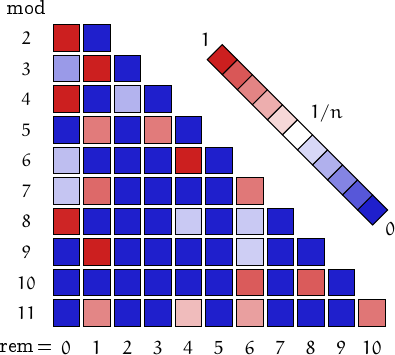

Perfect numbers can also be... (you may click on names or numbers)
aban
28
496
alternating
496
amenable
28
496
8128
33550336
apocalyptic
8128
binomial
28
496
8128
33550336
8589869056
137438691328
c.nonagonal
28
496
8128
33550336
8589869056
137438691328
canyon
8128
congruent
28
496
8128
Cunningham
28
fibodiv
28
frugal
33550336
happy
28
496
8128
harmonic
28
496
8128
33550336
8589869056
137438691328
Harshad
8589869056
hexagonal
28
496
8128
33550336
8589869056
137438691328
hyperperfect
28
496
8128
33550336
8589869056
137438691328
idoneal
28
metadrome
28
mountain
496
nude
8128
oban
28
odious
28
496
8128
33550336
pernicious
28
496
8128
plaindrome
28
practical
28
496
8128
productive
28
pseudoperfect
28
496
8128
33550336
repfigit
28
triangular
28
496
8128
33550336
8589869056
137438691328
uban
28
Ulam
28
8128
upside-down
28
wasteful
28
496
8128
Zumkeller
28
496
8128