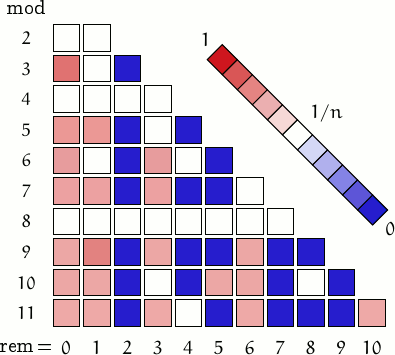
and
are among the simplest figurate numbers (see picture aside).
and
are among the simplest figurate numbers (see picture aside).
Gauss proved that every number is the sum of at most 3 triangular numbers. Ming showed that the only triangular numbers which are also Fibonacci numbers are 1, 3, 21 and 55.
N.Tzanahis B.M.M. de Weger proved that there are
six 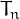 which are equal to the product
of 3 consecutive integers:
which are equal to the product
of 3 consecutive integers: 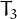 ,
, 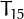 ,
,
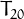 ,
, 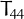 ,
, 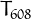 and
and
![\[T_{22736}=258474216=636\cdot 637\cdot638.\]](pic.8.png)
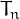 with palindromic index
are
with palindromic index
are 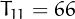 ,
, 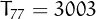 ,
, 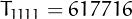 and
and
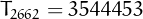 . The largest know such number, found by
P.De Geest, is
. The largest know such number, found by
P.De Geest, is 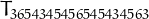 .
.
There are several interesting formulas involving triangular numbers, for example:
![\[
\begin{array}{lcl}
T_n+T_{n-1}=n^2\,, & & T_{2n}=3\cdot T_n+T_{n+1}\,,\\
T_n^2-T_{n-1}^2=n^3\,, & & T_{3n+1}=9\cdot T_n+1\,,\\
T_n^2=\sum_{k=1}^nk^3\,, &&
\int_0^1\int_0^1|x-y|^n\,dx\,dy=\frac{1}{T_{n+1}}\\
T_{k^2}=T_{k}^2+T_{k-1}^2\,,&
\end{array}
\]](pic.14.png)
The sum of the reciprocals of triangular number is 2.
By solving the diophantine equation 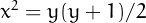 , it is easy to find infinite triangular numbers which are also square. The first are
1, 36, 1225, 41616,
1413721, 48024900, 1631432881, 55420693056,...
, it is easy to find infinite triangular numbers which are also square. The first are
1, 36, 1225, 41616,
1413721, 48024900, 1631432881, 55420693056,...
The 3 smallest primes which concatenated with the previous prime gives a triangular number are 1812341, 624403308264975451 and 48127684695939820823. For this 3rd value we have
![\[
\underline{48127684695939820823}\,\underline{48127684695939820753}=T_{98109820809070710302}.
\]](pic.16.png)
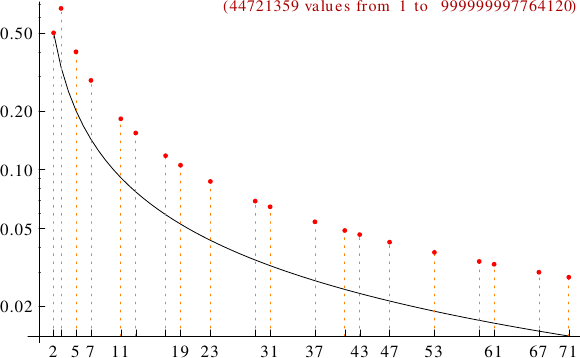
Below, the spiral pattern of triangular numbers up to  . See the page on prime numbers for an explanation and links to similar pictures.
. See the page on prime numbers for an explanation and links to similar pictures.
The first triangular numbers are 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300 more terms