A number is a metadrome in a given base 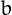 (often 10 or 16)
if its digits are in strictly increasing order in that base.
(often 10 or 16)
if its digits are in strictly increasing order in that base.
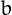 (often 10 or 16)
if its digits are in strictly increasing order in that base.
(often 10 or 16)
if its digits are in strictly increasing order in that base.
For example, 1234, 68 and 12789 are all metadromes in base 10.
If we allow the digits of a metadrome to be non-strictly increasing (i.e., nondecreasing, like in 1334558 or 2222, we obtain the plaindromes.
Similarly, the numbers whose digits are nonincreasing and strictly increasing are called nialpdromes and katadromes, respectively.
The total number metadromes in base 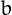 is equal to
is equal to 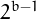 , hence in base
10 there are
, hence in base
10 there are 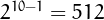 metadromes, from 0 to
123456789.
metadromes, from 0 to
123456789.
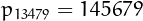 is the largest metadromic prime whose index is a metadrome too.
is the largest metadromic prime whose index is a metadrome too.
The first metadromes (in base 10) are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 13, 14, 15, 16, 17, 18, 19, 23, 24, 25, 26, 27, 28, 29, 34 more terms
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
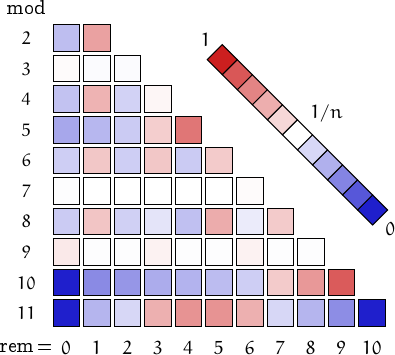

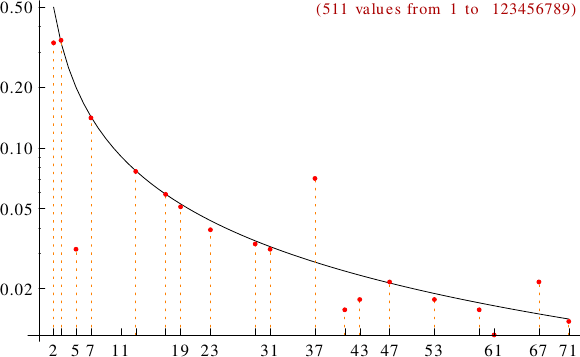
A graph displaying how many metadromes are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Metadromes can also be... (you may click on names or numbers and on + to get more values)
a-pointer
13
3469
123457
ABA
18
24
128
+
1568
aban
12
13
14
+
789
abundant
12
18
24
+
12345678
Achilles
1568
3456
12348
admirable
12
24
56
+
1234578
alt.fact.
19
alternating
12
14
16
+
123456789
amenable
12
13
16
+
123456789
apocalyptic
157
245
247
+
26789
arithmetic
13
14
15
+
3456789
astonishing
15
27
automorphic
25
balanced p.
157
257
1367
+
12356789
Bell
15
betrothed
48
binomial
15
28
35
+
2346
brilliant
14
15
25
+
234679
c.heptagonal
148
2458
c.nonagonal
28
136
1378
c.octagonal
25
49
169
+
134689
c.pentagonal
16
456
c.square
13
25
145
c.triangular
19
46
136
+
4789
cake
15
26
378
23479
Canada
125
Carol
47
Catalan
14
Chen
13
17
19
+
23456789
compositorial
24
congruent
13
14
15
+
3456789
constructible
12
15
16
+
257
cube
27
125
Cullen
25
Cunningham
15
17
24
+
13457
Curzon
14
18
26
+
12345678
cyclic
13
15
17
+
2356789
D-number
15
39
57
+
2346789
d-powerful
24
89
135
+
2456789
de Polignac
127
149
1259
+
23456789
decagonal
27
126
deceptive
259
12345679
deficient
13
14
15
+
3456789
dig.balanced
12
15
19
+
12345689
double fact.
15
48
Duffinian
16
25
27
+
2456789
eban
34
36
46
56
economical
13
14
15
+
13456789
emirp
13
17
37
+
1235789
emirpimes
15
26
39
+
12345789
enlightened
256
equidigital
13
14
15
+
13456789
eRAP
24
esthetic
12
23
34
+
123456789
Eulerian
26
57
247
evil
12
15
17
+
123456789
factorial
24
fibodiv
14
19
28
+
12356
Fibonacci
13
34
89
Friedman
25
125
126
+
235678
frugal
125
128
256
+
134689
gapful
135
1245
1278
+
12346789
Gilda
29
49
78
good prime
17
29
37
+
1245689
happy
13
19
23
+
3456789
harmonic
28
Harshad
12
18
24
+
12345679
heptagonal
18
34
148
+
1345789
hex
19
37
127
+
1234567
hexagonal
15
28
45
378
highly composite
12
24
36
48
hoax
58
136
234
+
12456789
Hogben
13
57
157
Honaker
457
12347
13457
house
78
hungry
17
hyperperfect
28
iban
12
14
17
+
12347
iccanobiF
13
39
124
idoneal
12
13
15
+
357
impolite
16
128
256
interprime
12
15
18
+
1345679
Jordan-Polya
12
16
24
+
3456
Kaprekar
45
Kynea
23
79
Lehmer
15
247
259
+
12346789
Leyland
17
57
145
368
lonely
23
Lucas
18
29
47
123
lucky
13
15
25
+
2345689
Lynch-Bell
12
15
24
+
1368
m-pointer
23
magic
15
34
369
1379
magnanimous
12
14
16
+
2489
modest
13
19
23
+
2678
Moran
18
27
45
+
12345679
Motzkin
127
nonagonal
24
46
nude
12
15
24
+
1368
O'Halloran
12
36
156
oban
12
13
15
+
789
odious
13
14
16
+
23456789
pancake
16
29
37
+
2347
panconsummate
12
14
15
+
267
pandigital
15
19
78
+
124689
partition
15
56
135
pentagonal
12
35
145
+
1247
perfect
28
pernicious
12
13
14
+
3456789
Perrin
12
17
29
+
367
Pierpont
13
17
19
+
3457
plaindrome
12
13
14
+
123456789
power
16
25
27
+
134689
powerful
16
25
27
+
134689
practical
12
16
18
+
1245678
prim.abundant
12
18
56
+
1234578
prime
13
17
19
+
23456789
primeval
13
37
137
+
12345679
pronic
12
56
156
Proth
13
17
25
+
13569
pseudoperfect
12
18
24
+
345678
repfigit
14
19
28
47
repunit
13
15
57
+
259
Rhonda
1568
Ruth-Aaron
15
16
24
+
369
self
345
356
367
+
12456789
semiprime
14
15
25
+
12345789
sliding
25
29
1258
15689
Smith
27
58
346
+
12456789
Sophie Germain
23
29
89
+
145679
sphenic
78
138
238
+
13456789
square
16
25
36
+
134689
star
13
37
straight-line
123
135
147
+
123456789
strobogrammatic
69
689
strong prime
17
29
37
+
1456789
super Niven
12
24
36
48
super-d
19
69
127
+
2346789
superabundant
12
24
36
48
tau
12
18
24
+
1234568
tetrahedral
35
56
tetranacci
15
29
56
triangular
15
28
36
+
2346
tribonacci
13
24
149
trimorphic
24
25
49
+
1249
truncatable prime
13
17
23
+
12347
twin
13
17
19
+
1245689
uban
12
13
15
+
89
Ulam
13
16
18
+
1234578
unprimeable
1268
1345
1346
+
2345678
untouchable
124
146
238
+
245678
upside-down
19
28
37
+
123456789
wasteful
12
18
24
+
3456789
weak prime
13
19
23
+
23456789
Woodall
17
23
159
Zuckerman
12
15
24
+
135
Zumkeller
12
24
28
+
45678