The first 600 lucky numbers :
1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, 87, 93, 99, 105, 111, 115, 127, 129, 133, 135, 141, 151, 159, 163, 169, 171, 189, 193, 195, 201, 205, 211, 219, 223, 231, 235, 237, 241, 259, 261, 267, 273, 283, 285, 289, 297, 303, 307, 319, 321, 327, 331, 339, 349, 357, 361, 367, 385, 391, 393, 399, 409, 415, 421, 427, 429, 433, 451, 463, 475, 477, 483, 487, 489, 495, 511, 517, 519, 529, 535, 537, 541, 553, 559, 577, 579, 583, 591, 601, 613, 615, 619, 621, 631, 639, 643, 645, 651, 655, 673, 679, 685, 693, 699, 717, 723, 727, 729, 735, 739, 741, 745, 769, 777, 781, 787, 801, 805, 819, 823, 831, 841, 855, 867, 873, 883, 885, 895, 897, 903, 925, 927, 931, 933, 937, 957, 961, 975, 979, 981, 991, 993, 997, 1009, 1011, 1021, 1023, 1029, 1039, 1041, 1053, 1057, 1087, 1093, 1095, 1101, 1105, 1107, 1117, 1123, 1147, 1155, 1167, 1179, 1183, 1189, 1197, 1201, 1203, 1209, 1219, 1231, 1233, 1245, 1249, 1251, 1261, 1263, 1275, 1281, 1285, 1291, 1303, 1309, 1323, 1329, 1339, 1357, 1365, 1369, 1387, 1389, 1395, 1401, 1417, 1419, 1435, 1441, 1455, 1459, 1471, 1473, 1485, 1491, 1495, 1497, 1501, 1503, 1519, 1533, 1543, 1545, 1563, 1567, 1575, 1579, 1585, 1587, 1597, 1599, 1611, 1639, 1641, 1645, 1659, 1663, 1675, 1693, 1701, 1705, 1711, 1723, 1731, 1737, 1749, 1765, 1767, 1771, 1773, 1777, 1797, 1801, 1809, 1819, 1827, 1831, 1833, 1839, 1857, 1869, 1879, 1893, 1899, 1915, 1921, 1923, 1933, 1941, 1945, 1959, 1963, 1965, 1977, 1983, 1987, 1995, 2001, 2019, 2023, 2031, 2053, 2059, 2065, 2067, 2079, 2083, 2085, 2095, 2113, 2115, 2121, 2125, 2127, 2133, 2163, 2173, 2187, 2209, 2211, 2215, 2217, 2221, 2239, 2251, 2253, 2257, 2271, 2277, 2281, 2283, 2301, 2311, 2317, 2323, 2335, 2343, 2355, 2365, 2379, 2395, 2403, 2407, 2409, 2415, 2419, 2427, 2439, 2445, 2461, 2467, 2473, 2479, 2491, 2493, 2505, 2511, 2523, 2527, 2545, 2557, 2563, 2571, 2575, 2587, 2589, 2593, 2599, 2607, 2625, 2635, 2647, 2649, 2653, 2661, 2667, 2671, 2689, 2697, 2715, 2725, 2755, 2763, 2773, 2781, 2785, 2787, 2797, 2815, 2817, 2821, 2823, 2827, 2835, 2841, 2845, 2851, 2877, 2887, 2899, 2901, 2905, 2913, 2923, 2943, 2953, 2961, 2971, 2973, 2977, 2983, 3003, 3007, 3027, 3031, 3037, 3039, 3049, 3055, 3073, 3075, 3091, 3097, 3099, 3109, 3111, 3121, 3123, 3133, 3153, 3163, 3171, 3175, 3183, 3187, 3199, 3213, 3223, 3229, 3235, 3243, 3259, 3261, 3289, 3297, 3301, 3307, 3313, 3325, 3339, 3351, 3355, 3363, 3381, 3403, 3405, 3409, 3411, 3427, 3433, 3439, 3451, 3453, 3465, 3477, 3481, 3487, 3489, 3495, 3499, 3507, 3559, 3565, 3571, 3579, 3595, 3597, 3603, 3607, 3613, 3621, 3625, 3633, 3655, 3661, 3663, 3669, 3675, 3685, 3687, 3697, 3709, 3717, 3721, 3727, 3747, 3753, 3763, 3771, 3781, 3789, 3793, 3795, 3811, 3843, 3847, 3849, 3865, 3873, 3879, 3889, 3891, 3897, 3909, 3915, 3931, 3943, 3951, 3955, 3969, 3975, 3981, 3991, 3999, 4003, 4015, 4023, 4033, 4035, 4041, 4045, 4063, 4069, 4081, 4095, 4105, 4107, 4129, 4131, 4161, 4165, 4173, 4179, 4189, 4195, 4201, 4203, 4207, 4227, 4237, 4251, 4255, 4257, 4263, 4269, 4285, 4287, 4315, 4321, 4329, 4335, 4363, 4377, 4383, 4389, 4399, 4413, 4431, 4441, 4443, 4455, 4461, 4465, 4483, 4485, 4495, 4509, 4519, 4521, 4539, 4551, 4561, 4567, 4569, 4573, 4587, 4609, 4611, 4621, 4623, 4629, 4645, 4647, 4653, 4663, 4671, 4675, 4695, 4699, 4713, 4717, 4725, 4741, 4761, 4767, 4773, 4797, 4801, 4809, 4813, 4819, 4833, 4837, 4839, 4843, 4851, 4863, 4867, 4881, 4887, 4893.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 609237 values, from 1 to 9999997).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0 | 609237 | 2 | ||||||||
| 3 | 305057 | 304180 | 0 | 3 | |||||||
| 4 | 0 | 304898 | 0 | 304339 | 4 | ||||||
| 5 | 121268 | 121583 | 122381 | 122907 | 121098 | 5 | |||||
| 6 | 0 | 304180 | 0 | 305057 | 0 | 0 | 6 | ||||
| 7 | 95430 | 95104 | 95241 | 114355 | 56710 | 57226 | 95171 | 7 | |||
| 8 | 0 | 152809 | 0 | 152093 | 0 | 152089 | 0 | 152246 | 8 | ||
| 9 | 95804 | 94972 | 0 | 95060 | 95098 | 0 | 114193 | 114110 | 0 | 9 | |
| 10 | 0 | 121583 | 0 | 122907 | 0 | 121268 | 0 | 122381 | 0 | 121098 | 10 |
| 11 | 55684 | 55401 | 55416 | 55485 | 55468 | 55399 | 55125 | 55365 | 55050 | 55646 | 55198 |
A pictorial representation of the table above
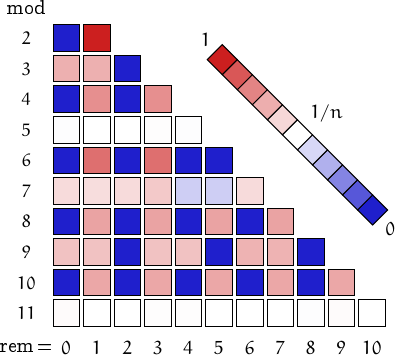
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits