• 72 can be written using four 4's:
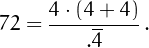
• Deleting all the even digits from 272 = 4722366482869645213696 we obtain a prime (7395139).
72 has 12 divisors (see below), whose sum is σ = 195. Its totient is φ = 24.
The previous prime is 71. The next prime is 73. The reversal of 72 is 27.
It is a powerful number, because all its prime factors have an exponent greater than 1 and also an Achilles number because it is not a perfect power.
It is a Jordan-Polya number, since it can be written as (3!)2 ⋅ 2!.
72 is nontrivially palindromic in base 5 and base 11.
It is an interprime number because it is at equal distance from previous prime (71) and next prime (73).
It can be written as a sum of positive squares in only one way, i.e., 36 + 36 = 6^2 + 6^2 .
It is a tau number, because it is divible by the number of its divisors (12).
It is an ABA number since it can be written as A⋅BA, here for A=2, B=6.
It is a Harshad number since it is a multiple of its sum of digits (9).
72 is an idoneal number.
It is an Ulam number.
It is an alternating number because its digits alternate between odd and even.
72 is an undulating number in base 5.
72 is a nontrivial repdigit in base 11.
It is a plaindrome in base 11, base 13, base 15 and base 16.
It is a nialpdrome in base 3, base 6, base 8, base 9, base 10, base 11, base 12 and base 14.
It is a zygodrome in base 3 and base 11.
It is a panconsummate number.
It is a pernicious number, because its binary representation contains a prime number (2) of ones.
It is a polite number, since it can be written in 2 ways as a sum of consecutive naturals, for example, 23 + 24 + 25.
72 is a droll number since its even prime factors and its odd prime factors have the same sum.
It is a pronic number, being equal to 8×9.
It is an amenable number.
It is a practical number, because each smaller number is the sum of distinct divisors of 72
72 is an abundant number, since it is smaller than the sum of its proper divisors (123).
It is a pseudoperfect number, because it is the sum of a subset of its proper divisors.
72 is a wasteful number, since it uses less digits than its factorization.
72 is an evil number, because the sum of its binary digits is even.
The sum of its prime factors is 12 (or 5 counting only the distinct ones).
The product of its digits is 14, while the sum is 9.
The square root of 72 is about 8.4852813742. The cubic root of 72 is about 4.1601676461.
Adding to 72 its reverse (27), we get a palindrome (99).
Subtracting from 72 its reverse (27), we obtain a triangular number (45 = T9).
The spelling of 72 in words is "seventy-two", and thus it is an aban number, an iban number, and an uban number.
• e-mail: info -at- numbersaplenty.com • Privacy notice • done in 0.081 sec. • engine limits •

