A number 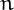 is a Leyland number if it can be written as
is a Leyland number if it can be written as
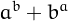 , with
, with 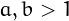 .
.
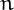 is a Leyland number if it can be written as
is a Leyland number if it can be written as
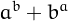 , with
, with 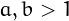 .
.
For example, 368 is a Leyland number because  .
.
Leyland numbers have been studied because some of them
are pretty large primes, like 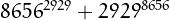 (30008 digits), or
(30008 digits), or
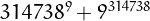 (300337 digits).
(300337 digits).
The first Leyland numbers are 8, 17, 32, 54, 57, 100, 145, 177, 320, 368, 512, 593, 945, 1124, 1649, 2169, 2530, 4240, 5392, 6250, 7073, 8361 more terms
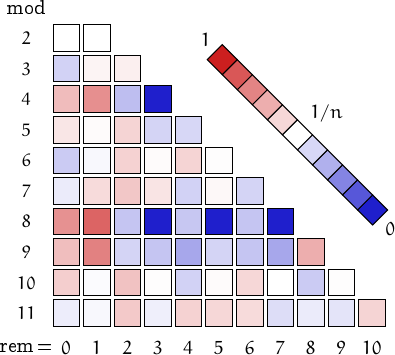
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

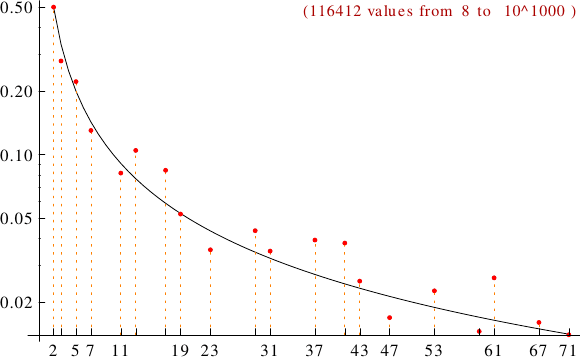
A graph displaying how many Leyland numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Leyland numbers can also be... (you may click on names or numbers and on + to get more values)
ABA
32
512
93312
33554432
774840978
20000000000
aban
17
32
54
57
100
145
+
20000000000
abundant
54
100
320
368
945
2530
+
14352282
Achilles
93312
20000000000
17832200896512
admirable
54
368
945
alternating
32
54
145
945
2169
8361
+
69632
amenable
17
32
57
100
145
177
+
536871753
apocalyptic
2530
4240
5392
6250
7073
8361
+
23401
arithmetic
17
54
57
145
177
593
+
9865625
balanced p.
593
32993
brilliant
1649
c.square
145
Chen
17
32993
congruent
54
145
320
368
1649
2530
+
9865625
constructible
17
32
320
512
65792
69632
+
281479271677952
cube
512
Cunningham
17
145
Curzon
54
593
1649
2169
18785
131361
+
177264449
cyclic
17
145
177
593
1649
7073
+
4785713
D-number
57
177
131361
423393
d-powerful
4240
262468
2097593
de Polignac
1649
32993
deficient
17
32
57
145
177
512
+
9865625
dig.balanced
177
2169
2530
60049
8389137
10609137
double fact.
945
Duffinian
32
57
100
512
1649
2169
+
8389137
eban
32
54
economical
17
32
145
177
320
512
+
16797952
emirp
17
emirpimes
177
7073
131361
equidigital
17
32
145
177
320
593
+
16777792
esthetic
32
54
Eulerian
57
evil
17
54
57
177
320
368
+
774840978
Friedman
93312
262468
533169
frugal
512
6250
93312
1647086
10609137
16797952
+
774840978
gapful
100
4240
16580
1048976
1058576
1596520
+
20000000000
good prime
17
593
happy
32
100
320
368
18785
60049
4194788
Harshad
54
100
320
512
2530
4240
+
2179768320
Hogben
57
house
32
hungry
17
iban
17
100
177
320
1124
4240
+
23401
idoneal
57
177
impolite
32
512
33554432
inconsummate
945
1649
20412
65792
131361
423393
Jordan-Polya
32
512
93312
33554432
17832200896512
junction
20412
94932
8389137
33554432
67109540
katadrome
32
54
320
lucky
131361
268705
magic
4294968320
magnanimous
32
512
metadrome
17
57
145
368
Moran
16580
nialpdrome
32
54
100
320
20000000000
nude
1124
93312
94932
oban
17
57
320
368
512
593
odious
32
100
145
512
4240
7073
+
387426321
panconsummate
54
57
pandigital
177
pentagonal
145
pernicious
17
100
145
320
4240
7073
+
9865625
Perrin
17
Pierpont
17
plaindrome
17
57
145
177
368
1124
power
32
100
512
33554432
powerful
32
100
512
93312
33554432
20000000000
17832200896512
practical
32
54
100
320
368
512
+
1941760
prim.abundant
368
945
2530
65792
prime
17
593
32993
2097593
8589935681
pronic
65792
4295032832
Proth
17
57
145
177
pseudoperfect
54
100
320
368
945
2530
+
94932
repunit
57
self
512
1649
6250
131361
10609137
268436240
semiprime
57
145
177
1649
7073
23401
+
43050817
sliding
20000000000
Smith
67137425
Sophie Germain
593
sphenic
60049
178478
268705
397585
524649
8389137
square
100
strong prime
17
2097593
super Niven
100
20000000000
super-d
2169
533169
1048976
1058576
1596520
tau
4240
20412
268436240
truncatable prime
17
593
twin
17
uban
17
32
57
20000000000
Ulam
57
145
177
2012174
unprimeable
320
512
16580
65792
69632
178478
+
1058576
untouchable
2530
16580
69632
93312
94932
178478
262468
upside-down
1649
wasteful
54
57
100
368
945
1124
+
8389137
Woodall
17
Zuckerman
93312
Zumkeller
54
320
368
945
2530
4240
+
94932