An integer 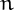 is called digitally powerful (here d-powerful) if it
can be expressed as a sum of positive powers of its digits.
is called digitally powerful (here d-powerful) if it
can be expressed as a sum of positive powers of its digits.
![\[3459872 = 3^1 + 4^6 + 5^5 + 9^6 + 8^3 + 7^7 + 2^{21}\]](pic.2.png) is d-powerful.
is d-powerful.
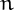 is called digitally powerful (here d-powerful) if it
can be expressed as a sum of positive powers of its digits.
is called digitally powerful (here d-powerful) if it
can be expressed as a sum of positive powers of its digits.
For example,
![\[3459872 = 3^1 + 4^6 + 5^5 + 9^6 + 8^3 + 7^7 + 2^{21}\]](pic.2.png)
Carlos Rivera (see link), who allows zero exponents, calls there numbers handsome.
The first d-powerful numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 24, 43, 63, 89, 132, 135, 153, 175, 209, 224, 226, 262, 264, 267, 283, 332, 333, 334, 357, 370, 371, 372, 373, 374, 375, 376, 377, 378, 379, 407, 445, 463, 518, 598, 629, 739, 794, 849, 935, 994 more terms
You can download a text file (d-powerful_up_1e6.txt, 0.9 MB), with a list of the 30067 d-powerful numbers up to 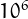 and the corresponding sums of powers.
and the corresponding sums of powers.
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
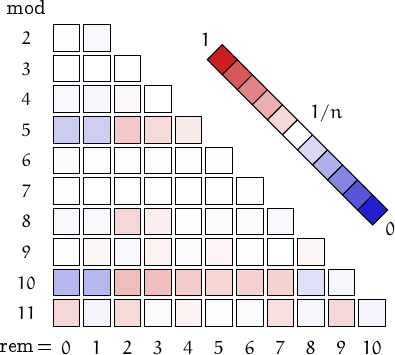

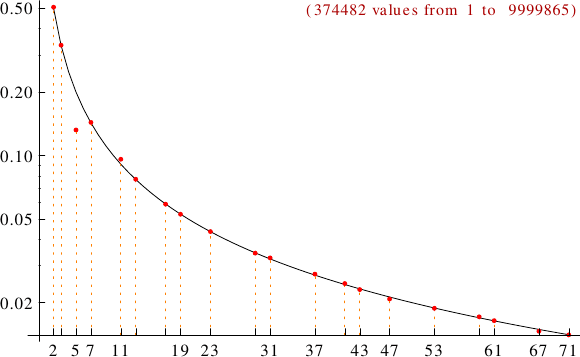
A graph displaying how many d-powerful numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

D-powerful numbers can also be... (you may click on names or numbers and on + to get more values)
ABA
24
375
2048
+
9954722
aban
24
43
63
+
7000895
abundant
24
132
224
+
9999752
Achilles
1323
5324
8712
+
9279432
admirable
24
224
1074
+
9996234
alternating
43
63
89
+
898729
amenable
24
89
132
+
9999865
amicable
783556
879712
2728726
+
7684672
apocalyptic
224
226
994
+
29967
arithmetic
43
89
132
+
9999865
astonishing
2132532
automorphic
376
balanced p.
373
17483
22447
+
9923477
binomial
153
378
1326
+
9792525
brilliant
209
377
407
+
9988337
c.decagonal
8201
249761
258781
+
4394531
c.heptagonal
43
463
2843
+
9442322
c.nonagonal
16471
24976
32896
+
7882435
c.octagonal
4225
5329
49729
+
8323225
c.pentagonal
226
3706
4951
+
9394456
c.square
2245
9385
24865
+
9843485
c.triangular
1306
2224
3385
+
9734635
cake
378
2048
2626
+
7207552
Carmichael
2465
278545
3146221
Catalan
132
Chen
89
379
2179
+
9979337
compositorial
24
congruent
24
63
135
+
9999423
constructible
24
1542
2048
+
7864320
cube
5832
35937
287496
+
4657463
Cullen
2228225
Cunningham
24
63
224
+
9865882
Curzon
89
153
209
+
9994326
cyclic
43
89
209
+
9999827
D-number
63
267
849
+
7040589
de Polignac
373
2203
2263
+
9994657
decagonal
175
370
2626
+
9457162
deceptive
231337
2358533
2392993
+
9567673
deficient
43
63
89
+
9999865
dig.balanced
135
153
209
+
9999827
droll
2240
4224
39424
Duffinian
63
175
209
+
9999865
eban
2062
2064
32052
+
4052036
economical
43
89
135
+
9997263
emirp
739
3257
3527
+
9984827
emirpimes
226
629
794
+
9992722
enlightened
2048
2238728
equidigital
43
89
135
+
9997263
eRAP
24
56563
78524
+
6275378
esthetic
43
89
1234
+
876543
evil
24
43
63
+
9999827
factorial
24
fibodiv
2733
24712
29923
+
209987
Fibonacci
89
377
Friedman
153
1255
2048
+
995346
frugal
2048
5329
23763
+
9822259
gapful
132
135
264
+
9999827
Gilda
65676
4848955
good prime
739
2063
2203
+
9887573
happy
226
262
376
+
9998724
Harshad
24
63
132
+
9998252
heptagonal
2205
2356
3940
+
9591264
hex
4447
22447
23497
+
9682237
hexagonal
153
378
1326
+
9792525
highly composite
24
hoax
1255
2064
2227
+
9992722
Hogben
43
463
2353
+
9526483
Honaker
2803
4153
4397
+
9972233
house
874234
2596375
9272286
hyperperfect
2133
10693
214273
296341
iban
24
43
224
+
777322
idoneal
24
357
impolite
2048
inconsummate
63
371
372
+
997784
interprime
334
370
376
+
9999227
Jacobsthal
43
2796203
Jordan-Polya
24
2048
24576
+
7864320
junction
1306
2315
2517
+
9997442
Kaprekar
2223
4950
356643
9372385
katadrome
43
63
5320
+
9876532
Lehmer
2465
3145
8245
+
9828295
Leyland
4240
262468
2097593
lonely
2179
1357265
4652430
Lucas
1364
lucky
43
63
135
+
9996789
Lynch-Bell
24
132
135
+
2189376
m-pointer
2131
magic
175
2465
66351
+
5848655
magnanimous
43
89
209
+
4488245
metadrome
24
89
135
+
2456789
modest
89
209
333
+
9865423
Moran
63
153
209
+
9998252
Motzkin
2356779
narcissistic
153
370
371
+
9926315
nialpdrome
43
63
332
+
9999865
nonagonal
24
4959
7944
+
8978409
nude
24
132
135
+
9983232
oban
63
89
333
+
935
octagonal
2133
2465
4485
+
8923425
odious
224
262
283
+
9999865
Ormiston
135497
235997
327779
+
9965479
palindromic
262
333
373
+
9859589
palprime
373
98389
3223223
+
9749479
pancake
379
407
4951
+
9642637
panconsummate
24
43
89
267
pandigital
135
1634
2134
+
9977513
partition
135
1255
2679689
pentagonal
376
3432
3725
+
9975572
pernicious
24
132
224
+
9999865
Perrin
209
2627
24914
Pierpont
3457
plaindrome
24
89
135
+
6667789
Poulet
2465
194221
223345
+
9567673
power
2048
4225
4624
+
9972964
powerful
1323
2048
4225
+
9972964
practical
24
132
224
+
9997668
prim.abundant
1074
1542
2205
+
9996234
prime
43
89
283
+
9993623
pronic
132
2352
6972
+
9837632
Proth
209
2241
2753
+
9875457
pseudoperfect
24
132
224
+
999252
repdigit
333
repfigit
62662
repunit
43
63
463
+
9573285
Rhonda
5832
196355
226953
+
9892552
Ruth-Aaron
24
153
370
+
9486722
Saint-Exupery
267540
self
132
209
334
+
9999752
semiprime
209
226
262
+
9999827
sliding
2225
22025
62660
+
3231250
Smith
378
1255
2227
+
9992762
Sophie Germain
89
2063
2753
+
9978833
sphenic
357
370
374
+
9999865
square
4225
4624
5329
+
9972964
star
2773
23437
26533
+
9563437
straight-line
135
333
357
+
876543
strong prime
379
739
2063
+
9993623
super Niven
24
8200
42240
262200
super-d
332
333
334
+
9995572
superabundant
24
tau
24
132
372
+
9995424
taxicab
32832
46683
525824
+
4624776
tetrahedral
366145
562475
657359
+
6435689
tetranacci
39648
2033628
triangular
153
378
1326
+
9792525
tribonacci
24
trimorphic
24
375
376
+
59375
truncatable prime
43
283
373
+
9979337
twin
43
283
463
+
9972583
uban
43
63
89
Ulam
175
209
370
+
9998724
undulating
262
373
2626
+
43434
unprimeable
518
1074
1672
+
9999752
untouchable
262
372
518
+
996732
upside-down
357
2738
4736
+
9785231
vampire
193257
263074
284598
729688
wasteful
24
63
132
+
9999865
weak prime
43
89
283
+
9979643
weakly prime
3326489
weird
9272
295330
338572
+
876964
Wieferich
22953
Woodall
63
4373
2359295
Zeisel
4293793
5069629
Zuckerman
24
132
135
+
6422976
Zumkeller
24
132
224
+
99402
zygodrome
333
2244
22333
+
9933222