J.-M. De Koninck and N. Doyon call a number 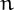
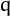 -esthetic
if the difference between adjacent digits is 1 when the number is written
in base
-esthetic
if the difference between adjacent digits is 1 when the number is written
in base 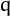 . For brevity, I omit the base when it is equal to 10.
. For brevity, I omit the base when it is equal to 10.
![\[
N_q(r)=\frac{2^r}{q+1}\sum_{\substack{k=1,\ k\ {\mathrm odd}\\[1mm]k\neq(q+1)/2}}^q%
\frac{\cos^r\alpha_k\cdot\sin^2\alpha_k}{(1-\cos\alpha_k)^2}\,,
\]](pic.8.png) where
where 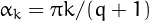 .
.
![\[
\begin{array}{rcl}
N_3(r) &\!\!\!=\!\!\!& 2^{r/2-2} ((3-2 \sqrt{2})(-1)^r+3+2 \sqrt{2})\,,\\
N_5(r) &\!\!\!=\!\!\!& 3^{r/2-1} ((7-4\sqrt{3}) (-1)^r+7+4 \sqrt{3})/2\,.
\end{array}
\]](pic.11.png) When
When 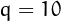 it is not possible to obtain a closed formula,
but the results of De Koninck & Doyon suggest a good approximation, i.e.,
it is not possible to obtain a closed formula,
but the results of De Koninck & Doyon suggest a good approximation, i.e.,
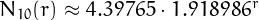 .
.
 -esthetic
if the difference between adjacent digits is 1 when the number is written
in base
-esthetic
if the difference between adjacent digits is 1 when the number is written
in base 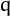 . For brevity, I omit the base when it is equal to 10.
. For brevity, I omit the base when it is equal to 10.
For example, 678989 is esthetic and 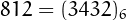 is
is 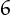 -esthetic.
-esthetic.
There are 17, 32, 61, 116, 222, 424, 813, 1556, and 2986 esthetic
numbers with 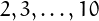 digits.
digits.
In general, De Koninck & Doyon have proved that the number 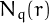 of the
of the
 -esthetic numbers of
-esthetic numbers of  digits is equal to
digits is equal to
![\[
N_q(r)=\frac{2^r}{q+1}\sum_{\substack{k=1,\ k\ {\mathrm odd}\\[1mm]k\neq(q+1)/2}}^q%
\frac{\cos^r\alpha_k\cdot\sin^2\alpha_k}{(1-\cos\alpha_k)^2}\,,
\]](pic.8.png)
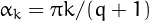 .
.
For some small values of 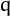 the expression above can be simplified.
For instance, we have
the expression above can be simplified.
For instance, we have 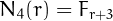 and
and
![\[
\begin{array}{rcl}
N_3(r) &\!\!\!=\!\!\!& 2^{r/2-2} ((3-2 \sqrt{2})(-1)^r+3+2 \sqrt{2})\,,\\
N_5(r) &\!\!\!=\!\!\!& 3^{r/2-1} ((7-4\sqrt{3}) (-1)^r+7+4 \sqrt{3})/2\,.
\end{array}
\]](pic.11.png)
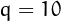 it is not possible to obtain a closed formula,
but the results of De Koninck & Doyon suggest a good approximation, i.e.,
it is not possible to obtain a closed formula,
but the results of De Koninck & Doyon suggest a good approximation, i.e.,
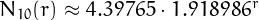 .
.
The first esthetic numbers (I disregard those smaller than 10) are 10, 12, 21, 23, 32, 34, 43, 45, 54, 56, 65, 67, 76, 78, 87, 89, 98, 101 more terms
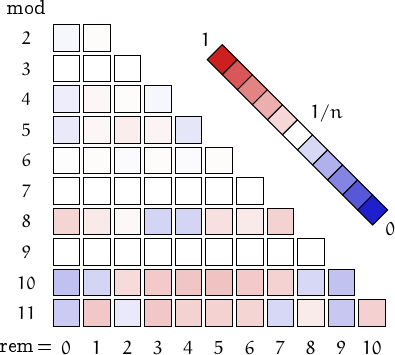
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

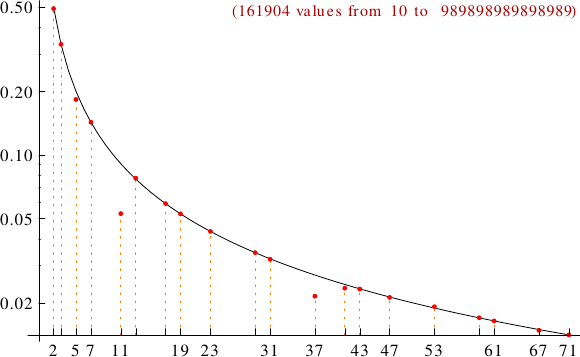
A graph displaying how many esthetic numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Useful links
Esthetic numbers can also be... (you may click on names or numbers and on + to get more values)
a-pointer
101
21212101
23210101
ABA
32
98
aban
10
12
21
+
989
abundant
12
54
56
+
43454565
Achilles
432
3456
admirable
12
54
56
+
98765454
alt.fact.
101
alternating
10
12
21
+
989898989
amenable
12
21
32
+
989898989
amicable
1210
apocalyptic
434
787
898
+
23456
arithmetic
21
23
43
+
9898989
automorphic
76
balanced p.
34543
432343
3212323
+
6789898987
binomial
10
21
45
+
5676765
brilliant
10
21
121
+
989878789
c.decagonal
101
2101
c.heptagonal
43
2101
c.nonagonal
10
c.octagonal
121
12321
1234321
+
123456787654321
c.pentagonal
76
456
c.square
545
c.triangular
10
45676
cake
232
Chen
23
67
89
+
67678789
congruent
21
23
34
+
9898989
constructible
10
12
32
34
cube
343
Cullen
65
Cunningham
10
65
101
+
123456765432101
Curzon
21
54
65
+
123434565
cyclic
23
43
65
+
9898789
D-number
21
87
123
+
5454321
d-powerful
43
89
1234
+
876543
de Polignac
4543
4567
8789
+
89878987
decagonal
10
232
deceptive
23212321
101010101
deficient
10
21
23
+
9898989
dig.balanced
10
12
21
+
65676565
Duffinian
21
32
65
+
9898987
eban
32
34
54
56
economical
10
21
23
+
12343454
emirp
12323
32321
1210123
+
121232101
emirpimes
123
321
1234
+
89876543
equidigital
10
21
23
+
12343454
eRAP
98
4345
evil
10
12
23
+
989898989
fibodiv
323
Fibonacci
21
34
89
+
6765
Friedman
121
343
12101
+
765432
frugal
343
76545
5456565
+
656543232
gapful
121
1010
1210
+
98987676567
Gilda
78
65676
good prime
67
101
happy
10
23
32
+
9878767
Harshad
10
12
21
+
9898987876
heptagonal
34
hex
1234567
hexagonal
45
5676765
highly composite
12
hoax
234
454
456
+
76545654
Hogben
21
43
343
10101
Honaker
34543
3212123
343456543
565454543
house
32
78
434
hyperperfect
21
iban
10
12
21
+
343212
idoneal
10
12
21
+
345
impolite
32
inconsummate
65
432
543
+
898787
interprime
12
21
34
+
98767878
Jacobsthal
21
43
Jordan-Polya
12
32
432
3456
junction
101
210
212
+
89898765
Kaprekar
45
katadrome
10
21
32
+
9876543210
Kynea
23
Lehmer
212323
Leyland
32
54
lonely
23
Lucas
76
123
lucky
21
43
67
+
9876787
Lynch-Bell
12
432
m-pointer
23
magic
34
65
magnanimous
12
21
23
+
101
metadrome
12
23
34
+
123456789
modest
23
89
545
+
1232121212
Moran
21
45
12345
+
98767678
Motzkin
21
323
nialpdrome
10
21
32
+
9876543210
nonagonal
123234
nude
12
212
432
+
434343432
O'Halloran
12
oban
10
12
23
+
989
octagonal
21
65
odious
21
32
56
+
989898789
palindromic
101
121
212
+
989898989898989
palprime
101
787
32323
+
989898787898989
pancake
56
67
121
+
2121234567676
panconsummate
10
12
21
+
121
pandigital
21
78
210
+
9876543210
partition
56
101
4565
pentagonal
12
210
3432
12345676565
pernicious
10
12
21
+
9898789
Perrin
10
12
persistent
9876543210
10123456789
89876543210
98765432101
plaindrome
12
23
34
+
123456789
power
32
121
343
+
1234567654321
powerful
32
121
343
+
123456787654321
practical
12
32
54
+
8765456
prim.abundant
12
56
78
+
98765454
prime
23
43
67
+
898989898987
primeval
10123
101234567
1012345678
10123456789
primorial
210
pronic
12
56
210
+
78987656
Proth
65
321
545
+
56565432321
pseudoperfect
12
54
56
+
989898
rare
65
repunit
21
43
121
+
101010101010101
Ruth-Aaron
78
self
121
323
345
+
989898789
semiprime
10
21
34
+
89878787
sliding
65
101
1010
Smith
121
454
654
+
98765432
Sophie Germain
23
89
12101
+
6787654343
sphenic
78
345
434
+
98987678
square
121
676
12321
+
123456787654321
star
121
straight-line
123
210
234
+
9876543210
strobogrammatic
101
10101
1010101
+
101010101010101
strong prime
67
101
787
+
89876767
super Niven
10
12
210
+
101010
super-d
454
5454
7656
+
9876545
superabundant
12
tau
12
56
232
+
898989876
tetrahedral
10
56
5456
6545
tetranacci
56
triangular
10
21
45
+
5676765
trimorphic
76
truncatable prime
23
43
67
twin
43
101
32321
+
345434567
uban
10
12
21
+
98
Ulam
87
434
456
+
8787898
undulating
101
121
212
+
989898989898989
unprimeable
898
3232
3234
+
9878765
untouchable
210
898
1212
+
987878
upside-down
456
654
34567
+
898987654321212
wasteful
12
34
45
+
9898989
weak prime
23
43
89
+
89876789
weird
343210
Woodall
23
323
Zeisel
1012121
Zuckerman
12
212
432
+
3232343232
Zumkeller
12
54
56
+
89898