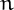 is panconsummate
if for every base
is panconsummate
if for every base 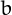 , there is a number
, there is a number 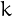 such that
such that 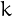 divided by
its sum of digits in base
divided by
its sum of digits in base 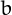 gives
gives 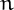 .
.
In other words, a number is panconsummate it is not inconsummate in any base.
Checking for this property is made easier by noting that a number 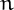 is always "consummate" in a base
is always "consummate" in a base 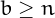 .
.
For example, 5 is panconsummate because
(a) 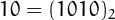 and
and 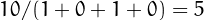 ,
(b)
,
(b) 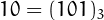 and
and 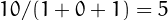 , and
(c)
, and
(c) 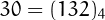 and
and 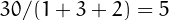 .
On the contrary, 62 is not panconsummate because in base 10 it does not exist a number
.
On the contrary, 62 is not panconsummate because in base 10 it does not exist a number 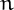 such that
such that 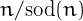 = 62 (i.e., 62 is inconsummate).
= 62 (i.e., 62 is inconsummate).
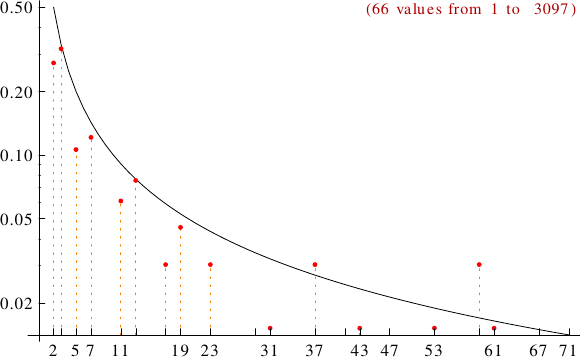
The known panconsummate numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 15, 18, 20, 21, 23, 24, 31, 34, 36, 37, 39, 40, 43, 45, 53, 54, 57, 59, 61, 69, 72, 73, 77, 78, 81, 85, 89, 91, 121, 127, 144, 166, 169, 211, 219, 231, 239, 257, 267, 271, 331, 337, 353, 361, 413, 481, 523, 571, 661, 721, 1093, 1291, 3097.
It there exist a further such number (which seems improbable),
it must be greater than 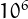 .
.