A number 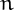 is a repunit in a base
is a repunit in a base 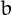 it all the digits in its representation in base
it all the digits in its representation in base 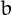 are equal to 1.
are equal to 1.
![\[
R_b(n) = \frac{b^n-1}{b-1}\,.
\]](pic.7.png)
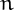 is a repunit in a base
is a repunit in a base 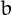 it all the digits in its representation in base
it all the digits in its representation in base 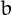 are equal to 1.
are equal to 1.
For example, 1, 1111, and 111111 are repunits in base 10, while 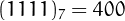 is a repunit in base 7.
is a repunit in base 7.
In general, a repunit  in base
in base  made of
made of 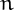 repetitions of the digit
repetitions of the digit  has value
has value
![\[
R_b(n) = \frac{b^n-1}{b-1}\,.
\]](pic.7.png)
The repdigits composed by repeated ones are called repunits.
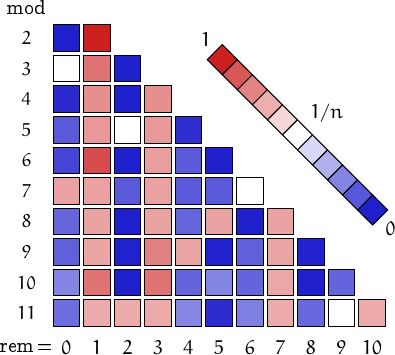
Since every number  can be represented as
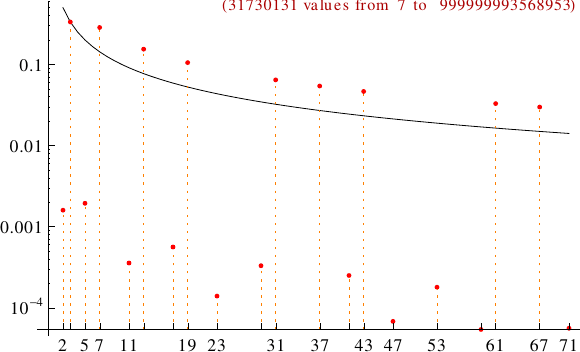
can be represented as 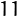 in base
in base 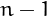 , I consider
only nontrivial repunits, i.e., those that contains at least 3 ones in some
base.
, I consider
only nontrivial repunits, i.e., those that contains at least 3 ones in some
base.
The first nontrivial repunits are , 13, 15, 21, 31, 40, 43, 57, 63, 73, 85, 91, 111, 121, 127, 133, 156, 157, 183, 211, 241, 255, 259, 273, 307, 341, 343, 364, 381, 400, 421more terms
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

A graph displaying how many repunits are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Repunits can also be... (you may click on names or numbers and on + to get more values)
a-pointer
13
24181
121453
+
9487636621
aban
13
15
21
+
999999000001
abundant
40
156
364
+
49565920
Achilles
7906143973
admirable
40
364
4095
alternating
21
43
63
+
981036363
amenable
13
21
40
+
999856021
apocalyptic
157
820
871
+
29757
arithmetic
13
15
21
+
9995083
astonishing
15
balanced p.
157
211
1123
+
9945973171
Bell
15
binomial
15
21
91
+
4734390674091
brilliant
15
21
121
+
999413383
c.decagonal
31
211
781
+
729500152756861
c.heptagonal
43
463
5461
+
300797044280503
c.nonagonal
91
703
820
+
231627523606480
c.octagonal
121
c.pentagonal
31
601
43891
+
131602780302451
c.square
13
85
421
+
745519146510613
c.triangular
31
85
2971
+
26835295698121
cake
15
Carmichael
5310721
2278677961
9593125081
29859667201
Chen
13
31
127
+
99790111
congruent
13
15
21
+
9969807
constructible
15
40
85
+
4294967295
cube
343
Cunningham
15
31
63
+
562949953421311
Curzon
21
273
341
+
199953741
cyclic
13
15
31
+
9982441
D-number
15
21
57
+
6993381
d-powerful
43
63
463
+
9573285
de Polignac
127
757
1807
+
99930013
decagonal
85
2047
1307020
deceptive
91
259
703
+
30244862011
deficient
13
15
21
+
9995083
dig.balanced
15
21
156
+
199812361
double fact.
15
Duffinian
21
57
63
+
9988761
eban
40
52060
economical
13
15
21
+
19994313
emirp
13
31
73
+
199162657
emirpimes
15
85
183
+
99810091
equidigital
13
15
21
+
19994313
eRAP
21058218111
esthetic
21
43
121
+
101010101010101
Eulerian
57
1191
evil
15
40
43
+
999792781
fibodiv
183
87321
Fibonacci
13
21
Friedman
121
127
343
+
597871
frugal
343
105301
179353
+
891589741
gapful
121
341
400
+
99992242441
Gilda
364
good prime
127
307
3907
+
196770757
happy
13
31
91
+
9988761
Harshad
21
40
63
+
9988303423
heptagonal
6175
18361
27931
+
29093062258603
hex
91
127
1261
+
346332937450507
hexagonal
15
91
703
+
160829915470003
hoax
85
364
1111
+
99351057
Hogben
13
21
31
+
999999993568953
Honaker
5701
8011
98911
+
975906361
hyperperfect
21
1333
16513
+
1951956868501
iban
21
40
43
+
777043
iccanobiF
13
idoneal
13
15
21
+
1365
inconsummate
63
381
553
+
995007
insolite
111
111111111
interprime
15
21
111
+
99450757
Jacobsthal
21
43
85
+
375299968947541
junction
111
307
507
+
99870043
Kaprekar
703
1111111111
katadrome
21
31
40
+
87321
Lehmer
15
85
91
+
984588837961
Leyland
57
lonely
211
lucky
13
15
21
+
9976123
Lynch-Bell
15
m-pointer
1123
magic
15
111
magnanimous
21
43
85
+
6007
metadrome
13
15
57
+
259
modest
13
111
133
+
1111111111
Moran
21
63
111
+
99390931
Motzkin
21
127
nialpdrome
21
31
40
+
111111111111111
nonagonal
111
651
99541
+
423236211589731
nude
15
111
1111
+
118612344
O'Halloran
156
oban
13
15
57
+
993
octagonal
21
40
133
+
375299968947541
odious
13
21
31
+
999982507
Ormiston
37831
530713
7681213
+
1997598331
palindromic
111
121
343
+
755971313179557
palprime
757
30103
pancake
121
211
781
+
372759573255307
panconsummate
15
21
31
+
1093
pandigital
15
21
156
+
15401701
partition
15
pentagonal
651
2380
5551
+
576009576039801
pernicious
13
21
31
+
9988761
persistent
10158926473
10865247933
12859673401
+
79865303421
Pierpont
13
73
plaindrome
13
15
57
+
111111111111111
Poulet
341
2047
4033
+
421925923038061
power
121
343
400
powerful
121
343
400
7906143973
practical
40
156
364
+
9984816
prim.abundant
364
4095
21562515
prime
13
31
43
+
999999000001
primeval
13
pronic
156
3906
97656
+
596046447753906
Proth
13
57
241
+
274877382657
pseudoperfect
40
156
364
+
980200
repdigit
111
1111
11111
+
111111111111111
Ruth-Aaron
15
154843
1236600
+
19369541451
Saint-Exupery
13709280
Sastry
183
40495
self
31
121
211
+
999160491
semiprime
15
21
57
+
99910021
sliding
133
Smith
85
121
1111
+
99351057
Sophie Germain
28792661
78914411
943280801
7294932341
sphenic
255
273
651
+
99950007
square
121
400
star
13
73
121
+
308836698141973
straight-line
111
1111
11111
+
111111111111111
strobogrammatic
111
1111
10101
+
111111111111111
strong prime
127
307
757
+
99211561
super Niven
40
400
super-d
31
127
381
+
9976123
tau
40
156
3280
+
943531280
taxicab
2436429101743
12166921836433
tetrahedral
364
tetranacci
15
triangular
15
21
91
+
231627523606480
tribonacci
13
truncatable prime
13
31
43
+
5113
twin
13
31
43
+
998907631
uban
13
15
21
+
96040049000007
Ulam
13
57
241
+
9894171
undulating
121
343
585
+
101010101010101
unprimeable
1464
3280
69905
+
9846355
untouchable
20440
60880
621436
+
866496
upside-down
73
91
41182996
98392919181721
wasteful
40
57
63
+
9995083
weak prime
13
31
43
+
99990001
weakly prime
23402421463
Wieferich
1093
22953
Woodall
63
1023
2047
+
137438953471
Zeisel
1885
Zuckerman
15
111
1111
+
1111111111
Zumkeller
40
156
364
+
97656
zygodrome
111
1111
11111
+
111111111111111