A prime  is said to be good if it
is said to be good if it
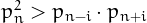 for every
for every 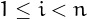 .
.
 is said to be good if it
is said to be good if it
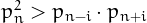 for every
for every 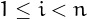 .
.
For example, 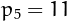 is a good prime since
is a good prime since
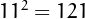 is greater than
is greater than 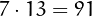 ,
, 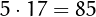 ,
, 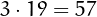 and
and 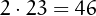 .
.
Carl Pomerance has proved that, as Selfrigde conjectured, there are infinite good primes.
The earliest runs of 2, 3,..., 7 consecutive good primes start at 37, 557, 1847, 216703, 6929381, 134193727, 15118087477 (this last value found by Jim Fougeron).
The first good primes are 5, 11, 17, 29, 37, 41, 53, 59, 67, 71, 97, 101, 127, 149, 179, 191, 223, 227, 251, 257, 269, 307, 311, 331, 347, 419, 431, 541, 557, 563, 569, 587, 593, 599, 641, 727, 733, 739, 809, 821, 853 more terms
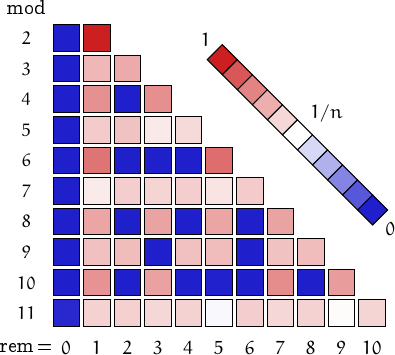
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

Useful links
Wikipedia, Good prime
Carl Pomerance,
The prime number graph, Math. Comp. 33 (1979), 399–408.
Carl Pomerance,
The prime number graph, Math. Comp. 33 (1979), 399–408.
Good primes can also be... (you may click on names or numbers and on + to get more values)
a-pointer
11
101
2521
5623
11657
+
198463511
aban
11
17
29
37
41
+
181000679
alt.fact.
101
alternating
29
41
67
101
127
+
189834389
amenable
17
29
37
41
53
+
199968469
apocalyptic
251
541
929
937
1031
+
29983
arithmetic
11
17
29
37
41
+
9993337
balanced p.
53
257
563
593
733
+
199880953
bemirp
10061
10091
19001
c.decagonal
11
101
2531
3251
3511
+
167360051
c.heptagonal
71
2647
50821
54251
139301
+
145857181
c.pentagonal
331
9151
143401
567631
28417531
+
146669851
c.square
41
1861
2521
26681
79601
+
140868113
c.triangular
4621
1173511
1358029
2552581
8904799
+
166368739
Carol
223
Chen
11
17
29
37
41
+
99927257
congruent
29
37
41
53
71
+
9993317
constructible
17
257
65537
Cunningham
17
37
101
127
257
+
139240001
Curzon
29
41
53
593
641
+
199883693
cyclic
11
17
29
37
41
+
9993337
d-powerful
739
2063
2203
2333
3167
+
9887573
de Polignac
127
149
251
331
599
+
99904457
deficient
11
17
29
37
41
+
9993337
dig.balanced
11
37
41
149
541
+
199784461
economical
11
17
29
37
41
+
19988359
emirp
17
37
71
97
149
+
199968443
equidigital
11
17
29
37
41
+
19988359
esthetic
67
101
Eulerian
11
65519
evil
17
29
53
71
101
+
199968443
fibodiv
149
Fibonacci
1597
Friedman
127
347
16879
48751
48757
+
937571
Gilda
29
happy
97
331
563
739
937
+
9993337
hex
37
127
331
4447
13669
+
169989769
Hogben
307
3907
6007
110557
288907
+
196770757
Honaker
3433
4903
6563
6653
7411
+
199022107
hungry
17
iban
11
17
41
71
101
+
747401
idoneal
37
inconsummate
431
563
821
1871
2609
+
999953
Jacobsthal
11
junction
101
307
311
1009
1213
+
99904439
katadrome
41
53
71
97
431
+
8521
Kynea
1087
263167
Leyland
17
593
lonely
53
Lucas
11
29
lucky
37
67
127
223
307
+
9993223
m-pointer
61211
312161
magnanimous
11
29
41
67
101
+
602081
metadrome
17
29
37
59
67
+
1245689
modest
29
59
311
599
733
+
172001287
Motzkin
127
nialpdrome
11
41
53
71
97
+
99754411
nude
11
oban
11
17
29
37
53
+
967
odious
11
37
41
59
67
+
199968539
Ormiston
40693
94397
112997
131413
131431
+
199882217
palindromic
11
101
191
727
929
+
195353591
palprime
11
101
191
727
929
+
195353591
pancake
11
29
37
67
191
+
186331861
panconsummate
11
37
53
59
127
+
331
pandigital
11
partition
11
101
pernicious
11
17
37
41
59
+
9993337
Perrin
17
29
853
Pierpont
17
37
97
257
3457
65537
plaindrome
11
17
29
37
59
+
133333777
prime
11
17
29
37
41
+
199968539
primeval
37
1367
13679
Proth
17
41
97
257
641
+
190857217
repdigit
11
repunit
127
307
3907
6007
110557
+
196770757
self
53
97
569
727
929
+
199883539
self-describing
12103331
sliding
11
29
101
641
Sophie Germain
11
29
41
53
179
+
199883693
star
37
541
937
2521
46993
+
114607621
strobogrammatic
11
101
119611
strong prime
11
17
29
37
41
+
99927257
super-d
127
269
331
419
431
+
9993019
tetranacci
29
tribonacci
149
trimorphic
251
truncatable prime
17
29
37
53
59
+
99537547
twin
11
17
29
41
59
+
199968539
uban
11
17
29
37
41
+
93000097
Ulam
11
53
97
431
739
+
9992681
undulating
101
191
727
929
upside-down
37
9371
1245689
33682477
91864291
98773321
weakly prime
5564453
59160317
61589579
126517543
Wieferich
3511
Woodall
17
191
Zuckerman
11
zygodrome
11
11777
33311
2244499
117770011