Search a number
lonely numbers
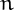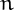A number  $n$  is called lonely if its distance to closest prime sets a new record.

For example, 0 is the first lonely number and has distance 2 from the first prime. The second lonely number is 23, which has a minimal distance 4, since the surrounding primes are 17 and 29. The third is 120 which has minimal distance 7, being sandwiched between the primes 113 and 127.

The first lonely numbers are 0, 23, 53, 120, 211, 1340, 1341, 1342, 1343, 1344, 2179, 3967, 15704, 15705, 16033, 19634, 19635, 24281, 31428, 31429, 31430, 31431, 31432, 31433, 38501 more terms

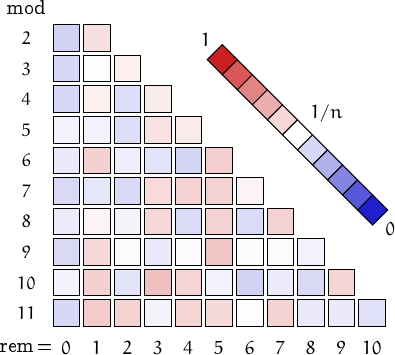
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
remainders of lonely numbers

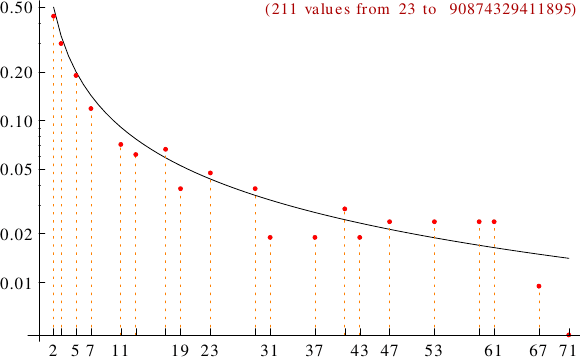
A graph displaying how many lonely numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
divisibility of lonely numbers
Useful links OEIS, Sequence A051650
Lonely numbers can also be... (you may click on names or numbers and on + to get more values)

aban 23 53 120 211 abundant 120 1340 + 4652430 20831424 20831426 47326800 admirable 120 alternating 23 38501 1272749 amenable 53 120 + 142414669 162821917 163710121 325737821 apocalyptic 1340 1341 + 16033 19634 19635 24281 arithmetic 23 53 + 2010806 4652428 4652429 4652430 balanced p. 53 211 binomial 120 brilliant 1343 c.decagonal 211 canyon 2179 Carol 3967 Chen 23 53 + 2179 24281 38501 1272749 congruent 23 53 + 2010806 2010807 4652429 4652430 constructible 120 Cunningham 120 Curzon 53 1341 + 31430 38501 492170 2010806 cyclic 23 53 + 1357267 2010803 2010805 4652429 D-number 31431 370317 d-powerful 2179 1357265 4652430 de Polignac 3967 24281 + 203713 206699 1272749 47326801 deficient 23 53 + 2010806 2010807 4652428 4652429 dig.balanced 120 15705 + 38501 203713 47326799 142414669 Duffinian 1343 31429 + 2010803 2010805 2010807 4652429 economical 23 53 + 1357267 2010803 10938023 12623189 emirp 1272749 162821917 emirpimes 1343 370313 370317 47326799 equidigital 23 53 + 1357267 2010803 10938023 12623189 esthetic 23 Eulerian 120 evil 23 53 + 47326803 142414669 162821917 163710121 factorial 120 gapful 120 1340 + 20831425 47326800 10726904850 25056082300 good prime 53 happy 23 15704 + 31433 370310 2010801 2010805 Harshad 120 1341 + 20831424 20831425 47326800 47326801 hexagonal 120 highly composite 120 hoax 1344 370316 4652428 47326803 Hogben 211 iban 23 120 + 370311 370312 370314 370317 idoneal 120 inconsummate 15704 15705 + 370313 370316 370317 492170 interprime 120 1344 + 2010807 4652430 20831428 47326803 Jordan-Polya 120 junction 58831 370313 + 20831422 20831424 20831426 20831428 katadrome 53 Kynea 23 lucky 211 31429 203713 370317 2010805 2010807 m-pointer 23 magnanimous 23 metadrome 23 modest 23 211 Moran 1341 mountain 120 1340 1341 1342 1343 nialpdrome 53 211 nude 1344 oban 23 53 odious 211 1341 + 47326801 47326802 122164858 325737821 pancake 211 panconsummate 23 53 211 pandigital 120 pernicious 211 1341 + 2010801 2010802 2010804 4652428 plaindrome 23 1344 practical 120 1344 15704 31428 2010800 prim.abundant 19635 prime 23 53 + 138465682247 313455525683 343834606051 491856414677 pseudoperfect 120 1340 + 31428 155964 370314 492170 repunit 211 self 53 211 + 4652428 4652430 20831425 20831427 semiprime 1343 19634 + 1357267 2010803 4652429 47326799 Smith 15704 47326803 Sophie Germain 23 53 24281 38501 10938023 sphenic 1342 370315 + 20831423 47326801 47326802 47326803 strong prime 16033 1272749 10938023 12623189 super Niven 120 super-d 24281 31431 58831 370310 superabundant 120 tau 1344 31432 47326800 tetrahedral 120 triangular 120 truncatable prime 23 53 3967 uban 23 53 Ulam 53 1340 + 370312 370315 370317 1357265 unprimeable 1340 1342 + 2010805 2010806 4652428 4652430 untouchable 120 1342 + 31430 155964 370310 370312 wasteful 120 1340 + 2010807 4652428 4652429 4652430 weak prime 23 2179 + 38501 58831 203713 206699 weird 31430 Woodall 23 Zuckerman 1344 Zumkeller 120 1340 + 15704 19635 31428 31430