A prime number 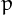 is called m-pointer if the next prime
number can be obtained adding
is called m-pointer if the next prime
number can be obtained adding 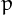 to its product of digits (here the 'm' stands for multiplicative).
to its product of digits (here the 'm' stands for multiplicative).
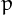 is called m-pointer if the next prime
number can be obtained adding
is called m-pointer if the next prime
number can be obtained adding 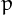 to its product of digits (here the 'm' stands for multiplicative).
to its product of digits (here the 'm' stands for multiplicative).
For example, 1231 is a m-pointer prime since the next prime is equal to 1231 + 1 ⋅ 2 ⋅ 3 ⋅ 1= 1237.
The first m-pointer primes are 23, 61, 1123, 1231, 1321, 2111, 2131, 11261, 11621, 12113, 13121, 15121, 19121, 21911, 22511, 27211, 61211, 116113, 131231, 312161, 611113, 1111211, 1111213, 1111361, 1112611, 1123151 more terms
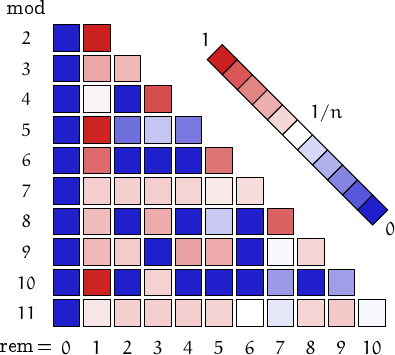
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

Useful links
OEIS, Sequence A089823
OEIS, Sequence A125840
Carlos Rivera, Puzzle 251. Pointer primes
OEIS, Sequence A125840
Carlos Rivera, Puzzle 251. Pointer primes
M-pointer primes can also be... (you may click on names or numbers and on + to get more values)
a-pointer
15121
aban
23
61
alternating
23
61
amenable
61
1321
11261
11621
12113
13121
15121
19121
116113
312161
+
119112113
121151341
131211181
211121213
apocalyptic
1321
2131
11261
11621
12113
13121
15121
19121
21911
22511
27211
arithmetic
23
61
1123
1231
1321
2111
2131
11261
11621
12113
+
3116111
3221111
4121113
9111341
balanced p.
1123
21911
3116111
11413111
12111331
14111311
316111111
1111131821
c.decagonal
61
c.square
61
Chen
23
2111
11261
11621
12113
13121
19121
21911
22511
61211
+
2121131
9111341
11922121
14111131
congruent
23
61
1231
1321
2111
11261
11621
21911
22511
131231
+
3112111
3116111
3221111
9111341
Curzon
1111361
9111341
cyclic
23
61
1123
1231
1321
2111
2131
11261
11621
12113
+
3116111
3221111
4121113
9111341
d-powerful
2131
de Polignac
15121
61211
1111211
13121117
61114211
deficient
23
61
1123
1231
1321
2111
2131
11261
11621
12113
+
3116111
3221111
4121113
9111341
dig.balanced
15121
2111411
2121131
11113321
11264111
13121117
61114211
136211111
163111111
economical
23
61
1123
1231
1321
2111
2131
11261
11621
12113
+
13121117
14111131
14111311
19122211
emirp
1231
1321
11621
12113
3112111
9111341
11264111
11413111
12111163
12111313
+
111111163
121115311
131261111
163111111
equidigital
23
61
1123
1231
1321
2111
2131
11261
11621
12113
+
13121117
14111131
14111311
19122211
esthetic
23
evil
23
11621
12113
13121
22511
27211
116113
312161
1112611
1123151
+
163111111
213111131
316111111
411221311
fibodiv
61
good prime
61211
312161
happy
23
2111
15121
116113
611113
1111211
hex
61
Hogben
1123
iban
23
1123
1321
2111
27211
inconsummate
11261
22511
61211
junction
2111
13121
15121
19121
22511
27211
61211
116113
611113
1112611
+
12111313
13121117
14111311
23311111
katadrome
61
Kynea
23
lonely
23
lucky
1123
1231
15121
4121113
magnanimous
23
61
metadrome
23
modest
23
2111
3221111
23311111
136211111
163111111
316111111
1312111111
nialpdrome
61
2111
3221111
oban
23
odious
61
1123
1231
1321
2111
2131
11261
15121
19121
21911
+
131211181
131261111
211121213
311221111
Ormiston
116113
611113
12111313
12111331
14111131
111131213
111611113
1161111113
palindromic
131121131
1116111116111
palprime
131121131
1116111116111
panconsummate
23
61
pernicious
61
1123
1231
1321
2111
2131
11261
15121
19121
61211
+
2111411
2121131
3116111
9111341
plaindrome
23
1123
prime
23
61
1123
1231
1321
2111
2131
11261
11621
12113
+
611121111143
611153111111
613511111111
711611111111
repfigit
61
repunit
1123
self
12113
1111213
11264111
61114211
121235111
131261111
136211111
Sophie Germain
23
1111361
3221111
9111341
121235111
1119413111
1121111531
1321141121
2232113111
4111311131
strong prime
2111
13121
15121
19121
61211
312161
1111211
1112611
1411411
1612111
+
11113321
11611121
14111131
23311111
super-d
1123
1231
2131
19121
131231
1123151
2121131
truncatable prime
23
12113
twin
61
1231
1321
2111
2131
611113
1111211
1111213
4121113
11314111
+
12111313
111219211
111316111
311221111
uban
23
61
Ulam
15121
19121
1111211
1111213
weak prime
23
61
1231
1321
2131
11261
11621
12113
22511
27211
+
12111313
13121117
19122211
61114211
Woodall
23