The first 600 super-d numbers :
19, 31, 69, 81, 105, 106, 107, 119, 127, 131, 169, 181, 190, 219, 231, 247, 261, 269, 281, 310, 318, 319, 331, 332, 333, 334, 335, 336, 337, 338, 339, 348, 369, 381, 419, 431, 454, 462, 469, 471, 481, 511, 519, 531, 558, 569, 581, 601, 619, 631, 669, 679, 681, 690, 715, 719, 731, 739, 749, 753, 769, 781, 782, 783, 784, 810, 819, 831, 869, 881, 919, 928, 931, 944, 969, 981, 988, 1019, 1031, 1036, 1046, 1049, 1050, 1051, 1052, 1053, 1054, 1055, 1056, 1057, 1058, 1059, 1060, 1061, 1062, 1063, 1064, 1065, 1066, 1067, 1068, 1069, 1070, 1071, 1072, 1081, 1119, 1123, 1131, 1145, 1168, 1169, 1181, 1188, 1190, 1219, 1231, 1269, 1270, 1281, 1310, 1319, 1331, 1369, 1377, 1381, 1419, 1431, 1453, 1454, 1469, 1471, 1481, 1487, 1512, 1519, 1531, 1556, 1569, 1581, 1616, 1617, 1619, 1631, 1645, 1669, 1681, 1690, 1719, 1731, 1752, 1761, 1764, 1769, 1778, 1781, 1792, 1810, 1819, 1831, 1847, 1848, 1869, 1881, 1900, 1901, 1919, 1923, 1926, 1931, 1965, 1968, 1969, 1981, 1989, 2019, 2028, 2031, 2046, 2069, 2081, 2119, 2124, 2131, 2148, 2152, 2159, 2169, 2181, 2182, 2190, 2219, 2231, 2232, 2261, 2269, 2281, 2310, 2319, 2331, 2363, 2369, 2373, 2381, 2395, 2419, 2421, 2431, 2462, 2469, 2470, 2471, 2472, 2473, 2474, 2475, 2476, 2477, 2478, 2479, 2481, 2519, 2531, 2532, 2569, 2571, 2581, 2591, 2610, 2619, 2627, 2631, 2667, 2669, 2681, 2690, 2719, 2731, 2759, 2769, 2781, 2810, 2818, 2819, 2831, 2848, 2869, 2881, 2919, 2926, 2931, 2935, 2943, 2954, 2969, 2981, 3011, 3019, 3031, 3035, 3058, 3069, 3081, 3084, 3087, 3100, 3119, 3131, 3148, 3163, 3169, 3172, 3180, 3181, 3190, 3219, 3231, 3239, 3258, 3269, 3281, 3310, 3317, 3318, 3319, 3320, 3321, 3322, 3323, 3324, 3325, 3326, 3327, 3328, 3329, 3330, 3331, 3332, 3333, 3334, 3335, 3336, 3337, 3338, 3339, 3340, 3341, 3342, 3343, 3344, 3345, 3346, 3347, 3348, 3349, 3350, 3351, 3352, 3353, 3354, 3355, 3356, 3357, 3358, 3359, 3360, 3361, 3362, 3363, 3364, 3365, 3366, 3367, 3368, 3369, 3370, 3371, 3372, 3373, 3374, 3375, 3376, 3377, 3378, 3379, 3380, 3381, 3382, 3383, 3384, 3385, 3386, 3387, 3388, 3389, 3390, 3391, 3408, 3419, 3431, 3444, 3469, 3471, 3480, 3481, 3488, 3494, 3519, 3531, 3542, 3569, 3581, 3619, 3621, 3623, 3631, 3669, 3681, 3690, 3719, 3731, 3769, 3781, 3783, 3810, 3819, 3829, 3831, 3851, 3855, 3868, 3869, 3877, 3881, 3884, 3919, 3931, 3951, 3969, 3981, 4012, 4013, 4014, 4015, 4016, 4017, 4018, 4019, 4031, 4056, 4069, 4076, 4081, 4119, 4131, 4137, 4143, 4169, 4181, 4190, 4197, 4219, 4231, 4256, 4261, 4269, 4281, 4285, 4310, 4314, 4319, 4331, 4369, 4372, 4381, 4419, 4431, 4451, 4469, 4471, 4479, 4481, 4489, 4519, 4527, 4531, 4540, 4546, 4554, 4569, 4581, 4594, 4595, 4596, 4597, 4598, 4602, 4611, 4619, 4620, 4631, 4638, 4649, 4652, 4669, 4681, 4682, 4690, 4710, 4719, 4731, 4732, 4755, 4769, 4781, 4794, 4797, 4806, 4807, 4808, 4809, 4810, 4819, 4823, 4831, 4854, 4869, 4873, 4881, 4895, 4919, 4931, 4961, 4966, 4969, 4972, 4981, 5011, 5019, 5031, 5036, 5049, 5061, 5069, 5081, 5105, 5109, 5110, 5111, 5112, 5113, 5119, 5127, 5131, 5169, 5181, 5190, 5207, 5219, 5226, 5231, 5247, 5269, 5281, 5302, 5310, 5318, 5319, 5331, 5342, 5348, 5349, 5369, 5381, 5414, 5419, 5431, 5454, 5469, 5471, 5481, 5501, 5511, 5517, 5519, 5531, 5533, 5558, 5569, 5577, 5578, 5579, 5580, 5581, 5619, 5623, 5631, 5645, 5649, 5667, 5669, 5681, 5687, 5690, 5715, 5719, 5731, 5739, 5769, 5781, 5810, 5819, 5831, 5869, 5881, 5919, 5931, 5944, 5969, 5981, 5988, 6009, 6010, 6011, 6012, 6019, 6031, 6051, 6059, 6069, 6081, 6092, 6096, 6119, 6123, 6131, 6133, 6145, 6169, 6181.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 1516453 values, from 19 to 9999981).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 588269 | 928184 | 2 | ||||||||
| 3 | 505703 | 505423 | 505327 | 3 | |||||||
| 4 | 278647 | 460983 | 309622 | 467201 | 4 | ||||||
| 5 | 242420 | 411717 | 228048 | 230582 | 403686 | 5 | |||||
| 6 | 196005 | 309242 | 196083 | 309698 | 196181 | 309244 | 6 | ||||
| 7 | 216899 | 216764 | 217163 | 216491 | 216288 | 216346 | 216502 | 7 | |||
| 8 | 137831 | 230203 | 154458 | 229223 | 140816 | 230780 | 155164 | 237978 | 8 | ||
| 9 | 169021 | 168360 | 168322 | 168246 | 168370 | 168477 | 168436 | 168693 | 168528 | 9 | |
| 10 | 133409 | 300677 | 114897 | 113090 | 111431 | 109011 | 111040 | 113151 | 117492 | 292255 | 10 |
| 11 | 137686 | 137961 | 138167 | 137731 | 137734 | 137526 | 137726 | 138019 | 137731 | 138054 | 138118 |
A pictorial representation of the table above
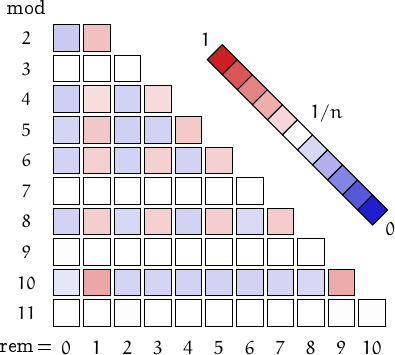
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits