The first 600 inconsummate numbers :
62, 63, 65, 75, 84, 95, 161, 173, 195, 216, 261, 266, 272, 276, 326, 371, 372, 377, 381, 383, 386, 387, 395, 411, 416, 422, 426, 431, 432, 438, 441, 443, 461, 466, 471, 476, 482, 483, 486, 488, 491, 492, 493, 494, 497, 498, 516, 521, 522, 527, 531, 533, 536, 542, 543, 546, 549, 552, 553, 563, 564, 573, 575, 612, 615, 620, 623, 630, 635, 639, 645, 650, 675, 716, 723, 750, 761, 771, 776, 785, 795, 816, 821, 822, 827, 831, 834, 839, 840, 845, 861, 866, 872, 876, 882, 926, 927, 932, 933, 936, 938, 941, 942, 945, 950, 966, 971, 972, 983, 986, 993, 1016, 1026, 1037, 1038, 1041, 1043, 1046, 1049, 1052, 1053, 1076, 1082, 1086, 1107, 1161, 1166, 1173, 1175, 1266, 1271, 1272, 1316, 1326, 1371, 1376, 1382, 1416, 1437, 1481, 1482, 1487, 1488, 1491, 1493, 1494, 1496, 1497, 1499, 1521, 1526, 1527, 1532, 1533, 1536, 1538, 1541, 1542, 1553, 1566, 1571, 1572, 1586, 1593, 1596, 1598, 1599, 1601, 1602, 1604, 1605, 1610, 1616, 1626, 1631, 1632, 1641, 1643, 1646, 1649, 1652, 1653, 1656, 1673, 1716, 1730, 1745, 1811, 1826, 1866, 1871, 1872, 1895, 1926, 1931, 1932, 1950, 1971, 1976, 1982, 1983, 1986, 2016, 2037, 2042, 2043, 2046, 2049, 2052, 2076, 2082, 2093, 2126, 2144, 2147, 2148, 2153, 2156, 2160, 2177, 2181, 2207, 2214, 2217, 2261, 2271, 2276, 2316, 2372, 2376, 2382, 2426, 2477, 2481, 2511, 2526, 2537, 2544, 2547, 2555, 2577, 2588, 2591, 2592, 2594, 2597, 2598, 2601, 2603, 2604, 2606, 2609, 2610, 2616, 2631, 2642, 2643, 2646, 2649, 2652, 2660, 2672, 2676, 2682, 2705, 2706, 2709, 2712, 2715, 2720, 2726, 2742, 2753, 2756, 2760, 2811, 2816, 2826, 2877, 2888, 2911, 2921, 2922, 2937, 2961, 2966, 2972, 2976, 2982, 2993, 3026, 3037, 3038, 3041, 3042, 3046, 3053, 3083, 3086, 3093, 3107, 3111, 3116, 3126, 3137, 3144, 3147, 3149, 3152, 3153, 3156, 3177, 3186, 3207, 3218, 3221, 3222, 3237, 3247, 3248, 3251, 3254, 3255, 3257, 3258, 3260, 3263, 3281, 3287, 3288, 3291, 3294, 3296, 3307, 3311, 3314, 3317, 3318, 3321, 3324, 3327, 3329, 3332, 3371, 3372, 3383, 3386, 3416, 3426, 3437, 3444, 3477, 3482, 3483, 3486, 3537, 3548, 3551, 3554, 3555, 3581, 3587, 3588, 3591, 3593, 3621, 3627, 3644, 3647, 3648, 3651, 3654, 3657, 3658, 3659, 3661, 3662, 3665, 3666, 3677, 3681, 3687, 3692, 3696, 3697, 3698, 3699, 3701, 3702, 3703, 3704, 3705, 3706, 3707, 3708, 3710, 3711, 3712, 3713, 3714, 3716, 3717, 3719, 3720, 3722, 3726, 3731, 3732, 3733, 3738, 3741, 3743, 3744, 3746, 3747, 3749, 3752, 3753, 3755, 3756, 3758, 3759, 3761, 3762, 3764, 3765, 3767, 3768, 3770, 3771, 3773, 3776, 3782, 3783, 3786, 3787, 3788, 3791, 3792, 3793, 3794, 3796, 3797, 3798, 3801, 3803, 3804, 3805, 3806, 3809, 3810, 3812, 3813, 3815, 3816, 3818, 3819, 3821, 3822, 3824, 3825, 3827, 3828, 3830, 3831, 3836, 3838, 3842, 3843, 3846, 3849, 3852, 3854, 3855, 3857, 3860, 3863, 3864, 3866, 3867, 3869, 3870, 3872, 3873, 3875, 3876, 3878, 3879, 3882, 3926, 3927, 3932, 3933, 3936, 3938, 3941, 3942, 3945, 3950, 3966, 3971, 3972, 3983, 3986, 3993, 4016, 4026, 4037, 4038, 4041, 4043, 4046, 4049, 4052, 4053, 4076, 4077, 4082, 4086, 4088, 4091, 4092, 4094, 4097, 4098, 4099, 4101, 4103, 4104, 4106, 4109, 4110, 4116, 4121, 4122, 4127, 4131, 4142, 4143, 4146, 4149, 4151, 4152, 4154, 4155, 4157, 4160, 4164, 4165, 4172, 4176, 4182, 4183, 4187, 4188, 4191, 4193, 4194, 4196, 4197, 4198, 4199, 4202, 4203, 4205, 4206, 4208, 4209, 4212, 4215, 4219, 4220, 4226, 4227, 4232, 4233, 4236, 4238, 4241, 4242, 4246, 4253, 4256, 4260, 4262, 4263, 4264, 4265, 4266, 4268, 4269, 4271, 4272, 4273, 4275, 4283, 4286, 4293, 4298, 4299.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 183089 values, from 62 to 999995).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 93279 | 89810 | 2 | ||||||||
| 3 | 89083 | 4700 | 89306 | 3 | |||||||
| 4 | 46368 | 46584 | 46911 | 43226 | 4 | ||||||
| 5 | 35485 | 34101 | 47318 | 30408 | 35777 | 5 | |||||
| 6 | 45517 | 2595 | 45657 | 43566 | 2105 | 43649 | 6 | ||||
| 7 | 26197 | 26151 | 26101 | 26203 | 26192 | 26150 | 26095 | 7 | |||
| 8 | 23201 | 23324 | 23591 | 21678 | 23167 | 23260 | 23320 | 21548 | 8 | ||
| 9 | 29658 | 2 | 29740 | 29709 | 2383 | 29774 | 29716 | 2315 | 29792 | 9 | |
| 10 | 16430 | 17832 | 20404 | 11910 | 21678 | 19055 | 16269 | 26914 | 18498 | 14099 | 10 |
| 11 | 15821 | 16706 | 16278 | 17210 | 18921 | 13108 | 17158 | 19473 | 15035 | 16803 | 16576 |
A pictorial representation of the table above
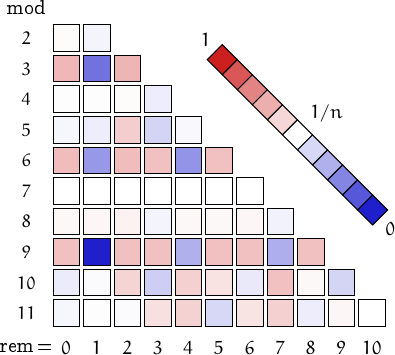
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits