Lucas numbers are defined by the recurrence 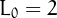 ,
, 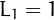 and
and 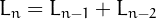 for
for  , so are similar to Fibonacci numbers, but with a different starting point.
, so are similar to Fibonacci numbers, but with a different starting point.
![\[L_n =\left(\frac{1+\sqrt{5}}{2}\right)^n+\left(\frac{1-\sqrt{5}}{2}\right)^n\]](pic.5.png)
![\[\sum_{k=1}^{\infty}\frac{L_k}{\alpha^k} = \frac{\alpha+2}{\alpha^2-\alpha-1}\,,\quad\quad \sum_{k=0}^{\infty}\frac{L_k}{k!} =\frac{1+e^{\sqrt{5}}}{\sqrt{e^{\sqrt{5}-1}}}\,.\]](pic.7.png)
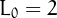 ,
, 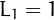 and
and 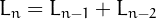 for
for  , so are similar to Fibonacci numbers, but with a different starting point.
, so are similar to Fibonacci numbers, but with a different starting point.
Their closed form is
![\[L_n =\left(\frac{1+\sqrt{5}}{2}\right)^n+\left(\frac{1-\sqrt{5}}{2}\right)^n\]](pic.5.png)
Two interesting sums (the first for any integer 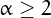 ):
):
![\[\sum_{k=1}^{\infty}\frac{L_k}{\alpha^k} = \frac{\alpha+2}{\alpha^2-\alpha-1}\,,\quad\quad \sum_{k=0}^{\infty}\frac{L_k}{k!} =\frac{1+e^{\sqrt{5}}}{\sqrt{e^{\sqrt{5}-1}}}\,.\]](pic.7.png)
The first Lucas numbers are 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207, 3571, 5778, 9349, 15127, 24476, 39603 more terms
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
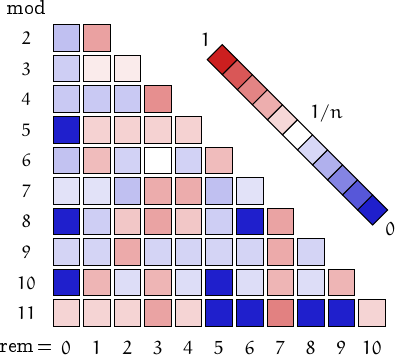

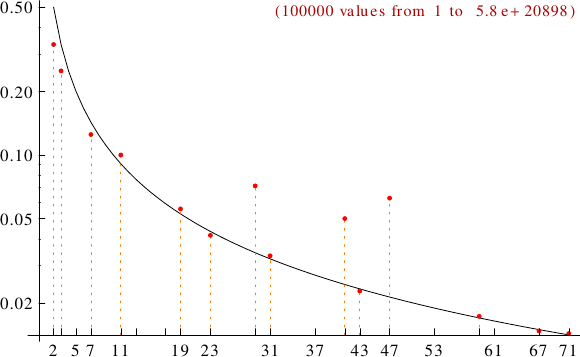
A graph displaying how many Lucas numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Lucas numbers can also be... (you may click on names or numbers and on + to get more values)
a-pointer
11
ABA
18
aban
11
18
29
47
76
123
199
322
521
843
abundant
18
5778
1860498
alternating
18
29
47
76
123
521
3010349
amenable
29
76
521
1364
9349
24476
167761
439204
3010349
7881196
54018521
141422324
969323029
apocalyptic
9349
15127
24476
arithmetic
11
29
47
123
199
322
521
843
1364
2207
+
710647
1149851
3010349
4870847
automorphic
76
binomial
5778
brilliant
64079
4870847
c.decagonal
11
c.pentagonal
76
c.triangular
199
Carol
47
Chen
11
29
47
199
521
2207
3010349
congruent
29
47
199
1364
2207
9349
15127
24476
64079
103682
710647
3010349
4870847
Curzon
18
29
3010349
54018521
cyclic
11
29
47
123
199
521
843
2207
3571
9349
+
167761
1149851
3010349
4870847
D-number
123
843
271443
d-powerful
1364
de Polignac
15127
54018521
deficient
11
29
47
76
123
199
322
521
843
1364
+
1149851
3010349
4870847
7881196
dig.balanced
11
167761
Duffinian
15127
39603
64079
167761
271443
1149851
4870847
economical
11
29
47
123
199
521
2207
3571
9349
15127
271443
1149851
3010349
12752043
emirp
199
3571
9349
3010349
emirpimes
123
15127
64079
equidigital
11
29
47
123
199
521
2207
3571
9349
15127
271443
1149851
3010349
12752043
esthetic
76
123
Eulerian
11
evil
18
29
123
843
5778
24476
103682
439204
1860498
54018521
599074578
fibodiv
47
199
Friedman
103682
gapful
167761
1860498
20633239
Gilda
29
2207
good prime
11
29
happy
1860498
Harshad
18
322
5778
heptagonal
18
hex
3571
hexagonal
5778
hoax
7881196
iban
11
47
123
322
2207
271443
idoneal
18
inconsummate
521
2207
103682
271443
interprime
18
76
1364
33385282
Jacobsthal
11
junction
521
katadrome
76
521
843
Lehmer
167761
lucky
3571
9349
710647
magnanimous
11
29
47
76
metadrome
18
29
47
123
modest
29
199
Moran
18
nialpdrome
11
76
322
521
843
nude
11
oban
11
18
29
76
odious
11
47
76
199
322
521
1364
2207
3571
9349
+
141422324
228826127
370248451
969323029
palindromic
11
167761
palprime
11
pancake
11
29
3571
panconsummate
11
18
pandigital
11
partition
11
pernicious
11
18
47
76
199
322
521
1364
2207
9349
+
271443
1149851
4870847
7881196
Perrin
29
plaindrome
11
18
29
47
123
199
5778
practical
18
5778
prim.abundant
18
prime
11
29
47
199
521
2207
3571
9349
3010349
54018521
370248451
6643838879
119218851371
pseudoperfect
18
5778
repdigit
11
repfigit
47
self
15127
39603
3010349
4870847
141422324
semiprime
123
843
15127
64079
271443
1149851
4870847
87403803
sliding
11
29
Sophie Germain
11
29
3010349
54018521
sphenic
322
39603
103682
167761
12752043
straight-line
123
strobogrammatic
11
strong prime
11
29
521
3571
54018521
super-d
15127
64079
1860498
3010349
7881196
tau
18
tetranacci
29
triangular
5778
trimorphic
76
truncatable prime
29
47
twin
11
29
199
521
uban
11
18
29
47
76
Ulam
11
18
47
167761
1149851
unprimeable
322
439204
1860498
untouchable
322
5778
wasteful
18
76
322
843
1364
5778
24476
39603
64079
103682
+
710647
1860498
4870847
7881196
weak prime
47
199
2207
9349
3010349
Zuckerman
11
Zumkeller
5778
zygodrome
11