A number 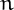 is a repdigit in a base
is a repdigit in a base 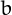 it all the digits in its representation in base
it all the digits in its representation in base 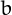 are equal.
are equal.
![\[
d \cdot \frac{b^n-1}{b-1}\,.
\]](pic.6.png)
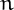 is a repdigit in a base
is a repdigit in a base 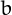 it all the digits in its representation in base
it all the digits in its representation in base 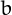 are equal.
are equal.
For example, 7, 222, and 88888 are repdigits in base 10, while 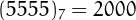 is a repdigit in base 7.
is a repdigit in base 7.
In general, a repdigit in base  made of
made of 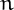 repetitions of the digit
repetitions of the digit 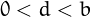 has value
has value
![\[
d \cdot \frac{b^n-1}{b-1}\,.
\]](pic.6.png)
The repdigits composed by repeated ones are called repunits.
A non-trivial repdigit is a number with at least two digits, however it must be noted that every number 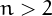 can be represented as
can be represented as 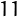 in base
in base 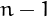 .
.
The first nontrivial repdigits in base 10 are 11, 22, 33, 44, 55, 66, 77, 88, 99, 111, 222, 333, 444, 555, 666, 777, 888, 999, 1111, 2222, 3333, 4444, 5555, 6666, 7777, 8888, 9999, 11111 more terms
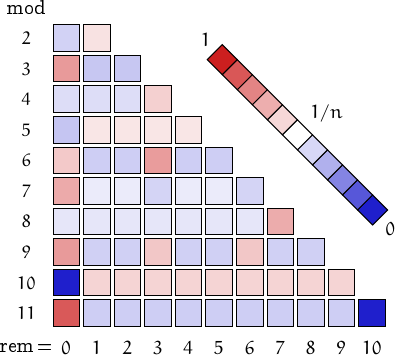
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

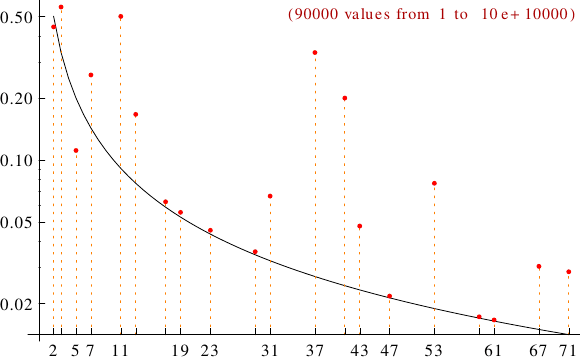
A graph displaying how many repdigits are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Repdigits can also be... (you may click on names or numbers and on + to get more values)
a-pointer
11
aban
11
22
33
44
55
66
+
999
abundant
66
88
222
444
666
888
+
6666666
admirable
66
88
222
amenable
33
44
77
88
333
444
+
888888888
apocalyptic
222
666
2222
3333
5555
6666
+
22222
arithmetic
11
22
33
44
55
66
+
9999999
binomial
55
66
666
c.decagonal
11
c.heptagonal
22
c.nonagonal
55
Chen
11
congruent
22
55
77
88
111
222
+
9999999
Cunningham
33
99
999
7777
9999
99999
+
99999999999999
Curzon
33
333333
33333333
cyclic
11
33
77
1111
3333
7777
+
5555555
D-number
33
111
d-powerful
333
de Polignac
11111111
deceptive
7777
11111
1111111
1111111111
11111111111
deficient
11
22
33
44
55
77
+
9999999
dig.balanced
11
44
99
555
666
2222
+
66666666
Duffinian
55
77
111
333
777
999
+
7777777
eban
44
66
economical
11
111
11111
1111111
equidigital
11
111
11111
1111111
Eulerian
11
66
evil
33
66
77
99
111
222
+
888888888
Fibonacci
55
gapful
1111
2222
3333
4444
5555
6666
+
9999999999
good prime
11
happy
44
888
5555
88888
1111111
2222222
Harshad
111
222
333
444
555
666
+
999999999
heptagonal
55
hexagonal
66
hoax
22
1111
6666666
Hogben
111
iban
11
22
44
77
111
222
+
777777
idoneal
22
33
88
insolite
111
111111111
interprime
99
111
4444
Jacobsthal
11
junction
111
11111
22222
222222
1111111
2222222
22222222
Kaprekar
55
99
999
7777
9999
22222
+
999999999999999
Lehmer
1111
Lucas
11
lucky
33
99
111
777
9999
33333
+
7777777
magic
111
magnanimous
11
modest
111
222
333
444
555
666
+
1111111111
Moran
111
222
333
444
555
666
+
999
nialpdrome
11
22
33
44
55
66
+
999999999999999
nonagonal
111
6666
nude
11
22
33
44
55
66
+
444444444
O'Halloran
44
oban
11
33
55
66
77
88
+
999
odious
11
22
44
55
88
333
+
999999999
palindromic
11
22
33
44
55
66
+
999999999999999
palprime
11
pancake
11
22
panconsummate
11
77
pandigital
11
99
partition
11
22
77
pentagonal
22
pernicious
11
22
33
44
55
66
+
6666666
Perrin
22
plaindrome
11
22
33
44
55
66
+
999999999999999
practical
66
88
666
888
6666
8888
+
888888
prim.abundant
66
88
222
999999
prime
11
Proth
33
pseudoperfect
66
88
222
444
666
888
+
999999
repunit
111
1111
11111
111111
1111111
11111111
+
111111111111111
Ruth-Aaron
77
self
222
1111
88888
111111
666666
7777777
+
555555555
self-describing
22
4444
666666
88888888
semiprime
22
33
55
77
111
1111
+
1111111
sliding
11
Smith
22
666
1111
6666666
Sophie Germain
11
sphenic
66
222
555
777
2222
3333
+
7777777
straight-line
111
222
333
444
555
666
+
999999999999999
strobogrammatic
11
88
111
888
1111
8888
+
888888888888888
strong prime
11
subfactorial
44
super-d
333
3333
33333
333333
3333333
tau
88
444
444444444
triangular
55
66
666
tribonacci
44
trimorphic
99
999
9999
99999
999999
9999999
+
999999999999999
twin
11
uban
11
22
33
55
66
77
+
99
Ulam
11
77
99
55555
2222222
9999999
unprimeable
55555
66666
222222
2222222
4444444
5555555
+
8888888
untouchable
88
66666
222222
upside-down
55
555
5555
55555
555555
5555555
+
555555555555555
wasteful
22
33
44
55
66
77
+
9999999
Woodall
99999999999
Zuckerman
11
111
1111
11111
111111
1111111
+
1111111111
Zumkeller
66
88
222
444
666
888
+
66666
zygodrome
11
22
33
44
55
66
+
999999999999999