The first 600 sphenic numbers :
30, 42, 66, 70, 78, 102, 105, 110, 114, 130, 138, 154, 165, 170, 174, 182, 186, 190, 195, 222, 230, 231, 238, 246, 255, 258, 266, 273, 282, 285, 286, 290, 310, 318, 322, 345, 354, 357, 366, 370, 374, 385, 399, 402, 406, 410, 418, 426, 429, 430, 434, 435, 438, 442, 455, 465, 470, 474, 483, 494, 498, 506, 518, 530, 534, 555, 561, 574, 582, 590, 595, 598, 602, 606, 609, 610, 615, 618, 627, 638, 642, 645, 646, 651, 654, 658, 663, 665, 670, 678, 682, 705, 710, 715, 730, 741, 742, 754, 759, 762, 777, 782, 786, 790, 795, 805, 806, 814, 822, 826, 830, 834, 854, 861, 874, 885, 890, 894, 897, 902, 903, 906, 915, 935, 938, 942, 946, 957, 962, 969, 970, 978, 986, 987, 994, 1001, 1002, 1005, 1010, 1015, 1022, 1023, 1030, 1034, 1038, 1045, 1054, 1065, 1066, 1070, 1074, 1085, 1086, 1090, 1095, 1102, 1105, 1106, 1113, 1118, 1130, 1131, 1146, 1158, 1162, 1166, 1173, 1178, 1182, 1185, 1194, 1209, 1221, 1222, 1235, 1239, 1245, 1246, 1258, 1265, 1266, 1270, 1281, 1295, 1298, 1309, 1310, 1311, 1334, 1335, 1338, 1342, 1353, 1358, 1362, 1370, 1374, 1378, 1390, 1394, 1398, 1406, 1407, 1414, 1419, 1426, 1434, 1435, 1442, 1443, 1446, 1455, 1462, 1463, 1474, 1479, 1490, 1491, 1495, 1498, 1505, 1506, 1510, 1515, 1526, 1533, 1534, 1542, 1545, 1547, 1551, 1558, 1562, 1570, 1578, 1581, 1582, 1586, 1595, 1598, 1599, 1605, 1606, 1614, 1615, 1626, 1630, 1634, 1635, 1645, 1653, 1659, 1662, 1670, 1677, 1686, 1695, 1698, 1702, 1705, 1729, 1730, 1738, 1742, 1743, 1749, 1758, 1767, 1771, 1778, 1786, 1790, 1798, 1802, 1810, 1826, 1833, 1834, 1842, 1846, 1855, 1866, 1869, 1878, 1885, 1886, 1887, 1898, 1902, 1905, 1910, 1918, 1930, 1946, 1947, 1955, 1958, 1965, 1970, 1978, 1986, 1990, 2001, 2006, 2013, 2014, 2015, 2022, 2035, 2037, 2054, 2055, 2065, 2067, 2074, 2082, 2085, 2086, 2091, 2093, 2094, 2109, 2110, 2114, 2118, 2121, 2134, 2135, 2139, 2146, 2154, 2158, 2162, 2163, 2185, 2193, 2198, 2202, 2211, 2222, 2230, 2233, 2235, 2238, 2242, 2247, 2255, 2261, 2265, 2266, 2270, 2274, 2278, 2282, 2289, 2290, 2294, 2298, 2301, 2314, 2318, 2330, 2334, 2337, 2338, 2343, 2345, 2354, 2355, 2365, 2373, 2378, 2379, 2382, 2387, 2390, 2397, 2398, 2405, 2406, 2409, 2410, 2414, 2422, 2431, 2438, 2445, 2451, 2454, 2465, 2482, 2485, 2486, 2494, 2505, 2506, 2510, 2514, 2522, 2526, 2534, 2542, 2546, 2553, 2555, 2570, 2585, 2586, 2595, 2598, 2607, 2613, 2626, 2630, 2634, 2635, 2639, 2658, 2665, 2666, 2667, 2674, 2678, 2679, 2685, 2686, 2690, 2694, 2697, 2698, 2702, 2703, 2710, 2714, 2715, 2717, 2726, 2737, 2739, 2742, 2751, 2755, 2758, 2765, 2766, 2769, 2770, 2774, 2778, 2782, 2786, 2794, 2795, 2802, 2806, 2810, 2821, 2822, 2829, 2830, 2834, 2847, 2849, 2865, 2874, 2877, 2882, 2895, 2905, 2914, 2915, 2919, 2922, 2930, 2937, 2938, 2945, 2946, 2954, 2955, 2967, 2985, 2994, 3002, 3009, 3014, 3018, 3021, 3026, 3034, 3054, 3055, 3058, 3059, 3070, 3074, 3081, 3082, 3110, 3111, 3115, 3122, 3126, 3129, 3130, 3138, 3145, 3154, 3157, 3165, 3170, 3171, 3178, 3182, 3201, 3206, 3219, 3237, 3243, 3245, 3246, 3262, 3266, 3278, 3282, 3286, 3289, 3297, 3298, 3302, 3310, 3311, 3322, 3333, 3335, 3342, 3345, 3346, 3355, 3358, 3363, 3367, 3370, 3374, 3378, 3382, 3395, 3399, 3405, 3406, 3414, 3417, 3422, 3423, 3426, 3434, 3435, 3441, 3445, 3451, 3454, 3462, 3470, 3471, 3477, 3478, 3485, 3490, 3495, 3502, 3507, 3514, 3515, 3522, 3526, 3530, 3531, 3535, 3538, 3553, 3558, 3562, 3565, 3567, 3585, 3586, 3590, 3594, 3597, 3598, 3605, 3606, 3614, 3615, 3619, 3621, 3633, 3634, 3638, 3642.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 20710806 values, from 30 to 99999994).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 7373736 | 13337070 | 2 | ||||||||
| 3 | 5318673 | 7696864 | 7695269 | 3 | |||||||
| 4 | 0 | 6669127 | 7373736 | 6667943 | 4 | ||||||
| 5 | 3420588 | 4322539 | 4321958 | 4323061 | 4322660 | 5 | |||||
| 6 | 1071203 | 4545229 | 3150898 | 4247470 | 3151635 | 4544371 | 6 | ||||
| 7 | 2529290 | 3029816 | 3030595 | 3029595 | 3030445 | 3030070 | 3030995 | 7 | |||
| 8 | 0 | 3334927 | 3686635 | 3334070 | 0 | 3334200 | 3687101 | 3333873 | 8 | ||
| 9 | 0 | 2565467 | 2565289 | 2659697 | 2566166 | 2564793 | 2658976 | 2565231 | 2565187 | 9 | |
| 10 | 664577 | 2645322 | 1676839 | 2645295 | 1677337 | 2756011 | 1677217 | 2645119 | 1677766 | 2645323 | 10 |
| 11 | 1671265 | 1904069 | 1904435 | 1903504 | 1903022 | 1904399 | 1903225 | 1905198 | 1903729 | 1903784 | 1904176 |
A pictorial representation of the table above
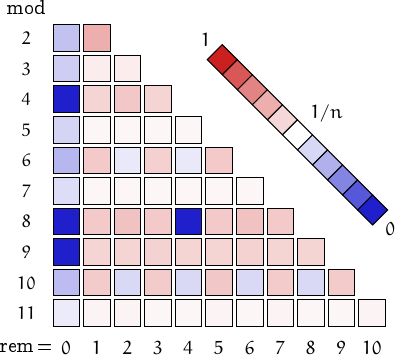
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits