The first 600 canyon numbers :
101, 102, 103, 104, 105, 106, 107, 108, 109, 201, 202, 203, 204, 205, 206, 207, 208, 209, 212, 213, 214, 215, 216, 217, 218, 219, 301, 302, 303, 304, 305, 306, 307, 308, 309, 312, 313, 314, 315, 316, 317, 318, 319, 323, 324, 325, 326, 327, 328, 329, 401, 402, 403, 404, 405, 406, 407, 408, 409, 412, 413, 414, 415, 416, 417, 418, 419, 423, 424, 425, 426, 427, 428, 429, 434, 435, 436, 437, 438, 439, 501, 502, 503, 504, 505, 506, 507, 508, 509, 512, 513, 514, 515, 516, 517, 518, 519, 523, 524, 525, 526, 527, 528, 529, 534, 535, 536, 537, 538, 539, 545, 546, 547, 548, 549, 601, 602, 603, 604, 605, 606, 607, 608, 609, 612, 613, 614, 615, 616, 617, 618, 619, 623, 624, 625, 626, 627, 628, 629, 634, 635, 636, 637, 638, 639, 645, 646, 647, 648, 649, 656, 657, 658, 659, 701, 702, 703, 704, 705, 706, 707, 708, 709, 712, 713, 714, 715, 716, 717, 718, 719, 723, 724, 725, 726, 727, 728, 729, 734, 735, 736, 737, 738, 739, 745, 746, 747, 748, 749, 756, 757, 758, 759, 767, 768, 769, 801, 802, 803, 804, 805, 806, 807, 808, 809, 812, 813, 814, 815, 816, 817, 818, 819, 823, 824, 825, 826, 827, 828, 829, 834, 835, 836, 837, 838, 839, 845, 846, 847, 848, 849, 856, 857, 858, 859, 867, 868, 869, 878, 879, 901, 902, 903, 904, 905, 906, 907, 908, 909, 912, 913, 914, 915, 916, 917, 918, 919, 923, 924, 925, 926, 927, 928, 929, 934, 935, 936, 937, 938, 939, 945, 946, 947, 948, 949, 956, 957, 958, 959, 967, 968, 969, 978, 979, 989, 1012, 1013, 1014, 1015, 1016, 1017, 1018, 1019, 1023, 1024, 1025, 1026, 1027, 1028, 1029, 1034, 1035, 1036, 1037, 1038, 1039, 1045, 1046, 1047, 1048, 1049, 1056, 1057, 1058, 1059, 1067, 1068, 1069, 1078, 1079, 1089, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2023, 2024, 2025, 2026, 2027, 2028, 2029, 2034, 2035, 2036, 2037, 2038, 2039, 2045, 2046, 2047, 2048, 2049, 2056, 2057, 2058, 2059, 2067, 2068, 2069, 2078, 2079, 2089, 2101, 2102, 2103, 2104, 2105, 2106, 2107, 2108, 2109, 2123, 2124, 2125, 2126, 2127, 2128, 2129, 2134, 2135, 2136, 2137, 2138, 2139, 2145, 2146, 2147, 2148, 2149, 2156, 2157, 2158, 2159, 2167, 2168, 2169, 2178, 2179, 2189, 3012, 3013, 3014, 3015, 3016, 3017, 3018, 3019, 3023, 3024, 3025, 3026, 3027, 3028, 3029, 3034, 3035, 3036, 3037, 3038, 3039, 3045, 3046, 3047, 3048, 3049, 3056, 3057, 3058, 3059, 3067, 3068, 3069, 3078, 3079, 3089, 3101, 3102, 3103, 3104, 3105, 3106, 3107, 3108, 3109, 3123, 3124, 3125, 3126, 3127, 3128, 3129, 3134, 3135, 3136, 3137, 3138, 3139, 3145, 3146, 3147, 3148, 3149, 3156, 3157, 3158, 3159, 3167, 3168, 3169, 3178, 3179, 3189, 3201, 3202, 3203, 3204, 3205, 3206, 3207, 3208, 3209, 3212, 3213, 3214, 3215, 3216, 3217, 3218, 3219, 3234, 3235, 3236, 3237, 3238, 3239, 3245, 3246, 3247, 3248, 3249, 3256, 3257, 3258, 3259, 3267, 3268, 3269, 3278, 3279, 3289, 4012, 4013, 4014, 4015, 4016, 4017, 4018, 4019, 4023, 4024, 4025, 4026, 4027, 4028, 4029, 4034, 4035, 4036, 4037, 4038, 4039, 4045, 4046, 4047, 4048, 4049, 4056, 4057, 4058, 4059, 4067, 4068, 4069, 4078, 4079, 4089, 4101, 4102, 4103, 4104, 4105, 4106, 4107, 4108, 4109, 4123, 4124, 4125, 4126, 4127, 4128, 4129, 4134, 4135, 4136, 4137, 4138, 4139, 4145, 4146, 4147, 4148, 4149, 4156, 4157, 4158, 4159, 4167, 4168, 4169, 4178, 4179, 4189, 4201, 4202, 4203, 4204, 4205, 4206, 4207, 4208, 4209, 4212, 4213, 4214, 4215, 4216, 4217, 4218, 4219, 4234, 4235, 4236, 4237, 4238.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 346484 values, from 101 to 987654323456789).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 115465 | 231019 | 2 | ||||||||
| 3 | 115555 | 115424 | 115505 | 3 | |||||||
| 4 | 46226 | 138607 | 69239 | 92412 | 4 | ||||||
| 5 | 10881 | 22287 | 44822 | 89668 | 178826 | 5 | |||||
| 6 | 38508 | 76984 | 38517 | 77047 | 38440 | 76988 | 6 | ||||
| 7 | 49502 | 49497 | 49492 | 49498 | 49499 | 49495 | 49501 | 7 | |||
| 8 | 27170 | 59918 | 29878 | 38101 | 19056 | 78689 | 39361 | 54311 | 8 | ||
| 9 | 38519 | 38470 | 38506 | 38516 | 38474 | 38498 | 38520 | 38480 | 38501 | 9 | |
| 10 | 0 | 511 | 1277 | 2681 | 5425 | 10881 | 21776 | 43545 | 86987 | 173401 | 10 |
| 11 | 51894 | 40940 | 27430 | 15755 | 9107 | 9059 | 15638 | 27375 | 41040 | 52039 | 56207 |
A pictorial representation of the table above
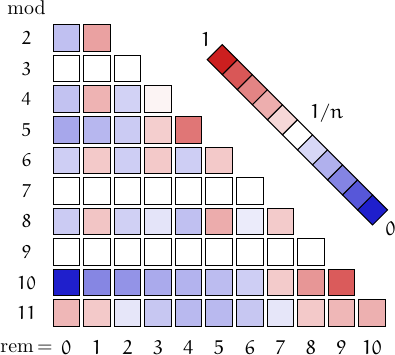
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits