The first 600 mountain numbers :
120, 121, 130, 131, 132, 140, 141, 142, 143, 150, 151, 152, 153, 154, 160, 161, 162, 163, 164, 165, 170, 171, 172, 173, 174, 175, 176, 180, 181, 182, 183, 184, 185, 186, 187, 190, 191, 192, 193, 194, 195, 196, 197, 198, 230, 231, 232, 240, 241, 242, 243, 250, 251, 252, 253, 254, 260, 261, 262, 263, 264, 265, 270, 271, 272, 273, 274, 275, 276, 280, 281, 282, 283, 284, 285, 286, 287, 290, 291, 292, 293, 294, 295, 296, 297, 298, 340, 341, 342, 343, 350, 351, 352, 353, 354, 360, 361, 362, 363, 364, 365, 370, 371, 372, 373, 374, 375, 376, 380, 381, 382, 383, 384, 385, 386, 387, 390, 391, 392, 393, 394, 395, 396, 397, 398, 450, 451, 452, 453, 454, 460, 461, 462, 463, 464, 465, 470, 471, 472, 473, 474, 475, 476, 480, 481, 482, 483, 484, 485, 486, 487, 490, 491, 492, 493, 494, 495, 496, 497, 498, 560, 561, 562, 563, 564, 565, 570, 571, 572, 573, 574, 575, 576, 580, 581, 582, 583, 584, 585, 586, 587, 590, 591, 592, 593, 594, 595, 596, 597, 598, 670, 671, 672, 673, 674, 675, 676, 680, 681, 682, 683, 684, 685, 686, 687, 690, 691, 692, 693, 694, 695, 696, 697, 698, 780, 781, 782, 783, 784, 785, 786, 787, 790, 791, 792, 793, 794, 795, 796, 797, 798, 890, 891, 892, 893, 894, 895, 896, 897, 898, 1210, 1230, 1231, 1232, 1240, 1241, 1242, 1243, 1250, 1251, 1252, 1253, 1254, 1260, 1261, 1262, 1263, 1264, 1265, 1270, 1271, 1272, 1273, 1274, 1275, 1276, 1280, 1281, 1282, 1283, 1284, 1285, 1286, 1287, 1290, 1291, 1292, 1293, 1294, 1295, 1296, 1297, 1298, 1310, 1320, 1321, 1340, 1341, 1342, 1343, 1350, 1351, 1352, 1353, 1354, 1360, 1361, 1362, 1363, 1364, 1365, 1370, 1371, 1372, 1373, 1374, 1375, 1376, 1380, 1381, 1382, 1383, 1384, 1385, 1386, 1387, 1390, 1391, 1392, 1393, 1394, 1395, 1396, 1397, 1398, 1410, 1420, 1421, 1430, 1431, 1432, 1450, 1451, 1452, 1453, 1454, 1460, 1461, 1462, 1463, 1464, 1465, 1470, 1471, 1472, 1473, 1474, 1475, 1476, 1480, 1481, 1482, 1483, 1484, 1485, 1486, 1487, 1490, 1491, 1492, 1493, 1494, 1495, 1496, 1497, 1498, 1510, 1520, 1521, 1530, 1531, 1532, 1540, 1541, 1542, 1543, 1560, 1561, 1562, 1563, 1564, 1565, 1570, 1571, 1572, 1573, 1574, 1575, 1576, 1580, 1581, 1582, 1583, 1584, 1585, 1586, 1587, 1590, 1591, 1592, 1593, 1594, 1595, 1596, 1597, 1598, 1610, 1620, 1621, 1630, 1631, 1632, 1640, 1641, 1642, 1643, 1650, 1651, 1652, 1653, 1654, 1670, 1671, 1672, 1673, 1674, 1675, 1676, 1680, 1681, 1682, 1683, 1684, 1685, 1686, 1687, 1690, 1691, 1692, 1693, 1694, 1695, 1696, 1697, 1698, 1710, 1720, 1721, 1730, 1731, 1732, 1740, 1741, 1742, 1743, 1750, 1751, 1752, 1753, 1754, 1760, 1761, 1762, 1763, 1764, 1765, 1780, 1781, 1782, 1783, 1784, 1785, 1786, 1787, 1790, 1791, 1792, 1793, 1794, 1795, 1796, 1797, 1798, 1810, 1820, 1821, 1830, 1831, 1832, 1840, 1841, 1842, 1843, 1850, 1851, 1852, 1853, 1854, 1860, 1861, 1862, 1863, 1864, 1865, 1870, 1871, 1872, 1873, 1874, 1875, 1876, 1890, 1891, 1892, 1893, 1894, 1895, 1896, 1897, 1898, 1910, 1920, 1921, 1930, 1931, 1932, 1940, 1941, 1942, 1943, 1950, 1951, 1952, 1953, 1954, 1960, 1961, 1962, 1963, 1964, 1965, 1970, 1971, 1972, 1973, 1974, 1975, 1976, 1980, 1981, 1982, 1983, 1984, 1985, 1986, 1987, 2310, 2320, 2321, 2340, 2341, 2342, 2343, 2350, 2351, 2352, 2353, 2354, 2360, 2361, 2362, 2363, 2364, 2365, 2370, 2371, 2372, 2373, 2374, 2375, 2376, 2380, 2381, 2382, 2383, 2384, 2385, 2386, 2387, 2390, 2391, 2392, 2393, 2394, 2395, 2396, 2397, 2398, 2410, 2420.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 173083 values, from 120 to 456789876543210).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 115465 | 57618 | 2 | ||||||||
| 3 | 57722 | 57701 | 57660 | 3 | |||||||
| 4 | 46124 | 34565 | 69341 | 23053 | 4 | ||||||
| 5 | 89437 | 44756 | 22353 | 11112 | 5425 | 5 | |||||
| 6 | 38508 | 19220 | 38476 | 19214 | 38481 | 19184 | 6 | ||||
| 7 | 24727 | 24730 | 24724 | 24720 | 24727 | 24728 | 24727 | 7 | |||
| 8 | 27122 | 19663 | 39423 | 9501 | 19002 | 14902 | 29918 | 13552 | 8 | ||
| 9 | 19240 | 19233 | 19222 | 19242 | 19232 | 19220 | 19240 | 19236 | 19218 | 9 | |
| 10 | 86732 | 43419 | 21716 | 10857 | 5425 | 2705 | 1337 | 637 | 255 | 0 | 10 |
| 11 | 30981 | 28195 | 21093 | 12762 | 6156 | 2742 | 2784 | 6246 | 12837 | 21108 | 28179 |
A pictorial representation of the table above
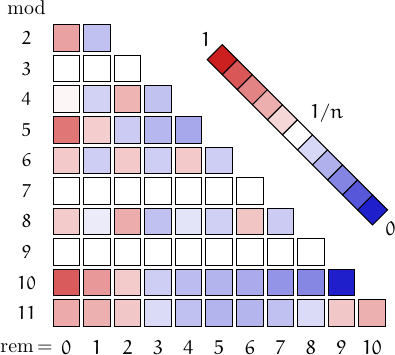
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits