The first 600 untouchable numbers :
2, 5, 52, 88, 96, 120, 124, 146, 162, 188, 206, 210, 216, 238, 246, 248, 262, 268, 276, 288, 290, 292, 304, 306, 322, 324, 326, 336, 342, 372, 406, 408, 426, 430, 448, 472, 474, 498, 516, 518, 520, 530, 540, 552, 556, 562, 576, 584, 612, 624, 626, 628, 658, 668, 670, 708, 714, 718, 726, 732, 738, 748, 750, 756, 766, 768, 782, 784, 792, 802, 804, 818, 836, 848, 852, 872, 892, 894, 896, 898, 902, 926, 934, 936, 964, 966, 976, 982, 996, 1002, 1028, 1044, 1046, 1060, 1068, 1074, 1078, 1080, 1102, 1116, 1128, 1134, 1146, 1148, 1150, 1160, 1162, 1168, 1180, 1186, 1192, 1200, 1212, 1222, 1236, 1246, 1248, 1254, 1256, 1258, 1266, 1272, 1288, 1296, 1312, 1314, 1316, 1318, 1326, 1332, 1342, 1346, 1348, 1360, 1380, 1388, 1398, 1404, 1406, 1418, 1420, 1422, 1438, 1476, 1506, 1508, 1510, 1522, 1528, 1538, 1542, 1566, 1578, 1588, 1596, 1632, 1642, 1650, 1680, 1682, 1692, 1716, 1718, 1728, 1732, 1746, 1758, 1766, 1774, 1776, 1806, 1816, 1820, 1822, 1830, 1838, 1840, 1842, 1844, 1852, 1860, 1866, 1884, 1888, 1894, 1896, 1920, 1922, 1944, 1956, 1958, 1960, 1962, 1972, 1986, 1992, 2008, 2010, 2022, 2024, 2036, 2048, 2050, 2052, 2058, 2062, 2068, 2078, 2096, 2098, 2108, 2118, 2120, 2128, 2136, 2148, 2152, 2158, 2168, 2174, 2178, 2190, 2196, 2198, 2212, 2218, 2226, 2228, 2232, 2248, 2258, 2262, 2302, 2304, 2306, 2316, 2322, 2324, 2330, 2338, 2356, 2364, 2366, 2376, 2388, 2404, 2408, 2410, 2416, 2422, 2430, 2432, 2436, 2446, 2452, 2454, 2464, 2482, 2484, 2490, 2496, 2498, 2500, 2502, 2514, 2518, 2530, 2564, 2568, 2572, 2576, 2586, 2588, 2590, 2600, 2602, 2606, 2608, 2614, 2628, 2640, 2642, 2704, 2718, 2724, 2726, 2736, 2748, 2758, 2760, 2762, 2766, 2774, 2784, 2788, 2808, 2824, 2828, 2850, 2856, 2874, 2876, 2894, 2902, 2914, 2922, 2932, 2944, 2946, 2950, 2952, 2968, 2978, 2982, 2984, 2992, 2994, 2996, 3008, 3018, 3028, 3036, 3060, 3072, 3076, 3078, 3102, 3104, 3114, 3126, 3132, 3136, 3142, 3144, 3152, 3156, 3162, 3174, 3186, 3198, 3202, 3208, 3228, 3234, 3236, 3238, 3246, 3266, 3270, 3276, 3278, 3292, 3296, 3306, 3312, 3318, 3328, 3340, 3356, 3366, 3378, 3384, 3388, 3396, 3400, 3402, 3406, 3412, 3420, 3422, 3428, 3430, 3432, 3448, 3454, 3476, 3484, 3486, 3488, 3504, 3506, 3510, 3524, 3538, 3556, 3564, 3576, 3580, 3588, 3590, 3592, 3600, 3604, 3630, 3636, 3642, 3648, 3650, 3652, 3656, 3666, 3670, 3682, 3684, 3708, 3738, 3744, 3746, 3748, 3752, 3758, 3760, 3774, 3786, 3788, 3792, 3808, 3812, 3816, 3818, 3820, 3828, 3832, 3842, 3860, 3862, 3868, 3872, 3876, 3888, 3900, 3902, 3904, 3936, 3940, 3942, 3954, 3958, 3960, 3972, 3974, 3982, 3986, 4018, 4026, 4032, 4036, 4046, 4048, 4056, 4062, 4068, 4070, 4072, 4078, 4086, 4088, 4098, 4104, 4116, 4120, 4148, 4168, 4170, 4172, 4184, 4188, 4190, 4198, 4206, 4216, 4224, 4238, 4248, 4258, 4268, 4280, 4296, 4302, 4304, 4308, 4312, 4316, 4318, 4320, 4322, 4336, 4344, 4356, 4368, 4370, 4380, 4382, 4386, 4388, 4396, 4402, 4406, 4416, 4430, 4462, 4472, 4476, 4480, 4488, 4490, 4492, 4498, 4500, 4506, 4512, 4530, 4534, 4574, 4580, 4588, 4612, 4614, 4618, 4630, 4648, 4662, 4668, 4672, 4678, 4686, 4688, 4690, 4700, 4710, 4712, 4718, 4738, 4740, 4742, 4748, 4750, 4758, 4764, 4770, 4772, 4782, 4808, 4830, 4838, 4840, 4842, 4850, 4854, 4856, 4860, 4868, 4882, 4884, 4886, 4896, 4898, 4908, 4914, 4916, 4926, 4928, 4942, 4956, 4962, 4964, 4980, 4982, 4984, 4998, 5016, 5030, 5032, 5034, 5044, 5070, 5072, 5092, 5094, 5096, 5106, 5126, 5132, 5136, 5138, 5142, 5144, 5152, 5158, 5160, 5178, 5184, 5202, 5204, 5208, 5214, 5218, 5222, 5224, 5226.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 150232 values, from 2 to 999996).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 150231 | 1 | 2 | ||||||||
| 3 | 65349 | 41873 | 43010 | 3 | |||||||
| 4 | 83603 | 1 | 66628 | 0 | 4 | ||||||
| 5 | 27675 | 35525 | 31933 | 33931 | 21168 | 5 | |||||
| 6 | 65349 | 0 | 43009 | 0 | 41873 | 1 | 6 | ||||
| 7 | 22234 | 20439 | 18186 | 26415 | 19465 | 22166 | 21327 | 7 | |||
| 8 | 43456 | 0 | 28609 | 0 | 40147 | 1 | 38019 | 0 | 8 | ||
| 9 | 21584 | 11939 | 14267 | 26997 | 13237 | 14331 | 16768 | 16697 | 14412 | 9 | |
| 10 | 27674 | 0 | 31933 | 0 | 21168 | 1 | 35525 | 0 | 33931 | 0 | 10 |
| 11 | 13257 | 17921 | 13451 | 15246 | 13485 | 11571 | 13536 | 14376 | 13084 | 11725 | 12580 |
A pictorial representation of the table above
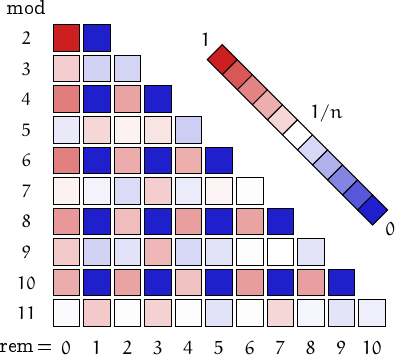
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits