The first 600 evil numbers :
3, 5, 6, 9, 10, 12, 15, 17, 18, 20, 23, 24, 27, 29, 30, 33, 34, 36, 39, 40, 43, 45, 46, 48, 51, 53, 54, 57, 58, 60, 63, 65, 66, 68, 71, 72, 75, 77, 78, 80, 83, 85, 86, 89, 90, 92, 95, 96, 99, 101, 102, 105, 106, 108, 111, 113, 114, 116, 119, 120, 123, 125, 126, 129, 130, 132, 135, 136, 139, 141, 142, 144, 147, 149, 150, 153, 154, 156, 159, 160, 163, 165, 166, 169, 170, 172, 175, 177, 178, 180, 183, 184, 187, 189, 190, 192, 195, 197, 198, 201, 202, 204, 207, 209, 210, 212, 215, 216, 219, 221, 222, 225, 226, 228, 231, 232, 235, 237, 238, 240, 243, 245, 246, 249, 250, 252, 255, 257, 258, 260, 263, 264, 267, 269, 270, 272, 275, 277, 278, 281, 282, 284, 287, 288, 291, 293, 294, 297, 298, 300, 303, 305, 306, 308, 311, 312, 315, 317, 318, 320, 323, 325, 326, 329, 330, 332, 335, 337, 338, 340, 343, 344, 347, 349, 350, 353, 354, 356, 359, 360, 363, 365, 366, 368, 371, 373, 374, 377, 378, 380, 383, 384, 387, 389, 390, 393, 394, 396, 399, 401, 402, 404, 407, 408, 411, 413, 414, 417, 418, 420, 423, 424, 427, 429, 430, 432, 435, 437, 438, 441, 442, 444, 447, 449, 450, 452, 455, 456, 459, 461, 462, 464, 467, 469, 470, 473, 474, 476, 479, 480, 483, 485, 486, 489, 490, 492, 495, 497, 498, 500, 503, 504, 507, 509, 510, 513, 514, 516, 519, 520, 523, 525, 526, 528, 531, 533, 534, 537, 538, 540, 543, 544, 547, 549, 550, 553, 554, 556, 559, 561, 562, 564, 567, 568, 571, 573, 574, 576, 579, 581, 582, 585, 586, 588, 591, 593, 594, 596, 599, 600, 603, 605, 606, 609, 610, 612, 615, 616, 619, 621, 622, 624, 627, 629, 630, 633, 634, 636, 639, 640, 643, 645, 646, 649, 650, 652, 655, 657, 658, 660, 663, 664, 667, 669, 670, 673, 674, 676, 679, 680, 683, 685, 686, 688, 691, 693, 694, 697, 698, 700, 703, 705, 706, 708, 711, 712, 715, 717, 718, 720, 723, 725, 726, 729, 730, 732, 735, 736, 739, 741, 742, 745, 746, 748, 751, 753, 754, 756, 759, 760, 763, 765, 766, 768, 771, 773, 774, 777, 778, 780, 783, 785, 786, 788, 791, 792, 795, 797, 798, 801, 802, 804, 807, 808, 811, 813, 814, 816, 819, 821, 822, 825, 826, 828, 831, 833, 834, 836, 839, 840, 843, 845, 846, 848, 851, 853, 854, 857, 858, 860, 863, 864, 867, 869, 870, 873, 874, 876, 879, 881, 882, 884, 887, 888, 891, 893, 894, 897, 898, 900, 903, 904, 907, 909, 910, 912, 915, 917, 918, 921, 922, 924, 927, 928, 931, 933, 934, 937, 938, 940, 943, 945, 946, 948, 951, 952, 955, 957, 958, 960, 963, 965, 966, 969, 970, 972, 975, 977, 978, 980, 983, 984, 987, 989, 990, 993, 994, 996, 999, 1000, 1003, 1005, 1006, 1008, 1011, 1013, 1014, 1017, 1018, 1020, 1023, 1025, 1026, 1028, 1031, 1032, 1035, 1037, 1038, 1040, 1043, 1045, 1046, 1049, 1050, 1052, 1055, 1056, 1059, 1061, 1062, 1065, 1066, 1068, 1071, 1073, 1074, 1076, 1079, 1080, 1083, 1085, 1086, 1088, 1091, 1093, 1094, 1097, 1098, 1100, 1103, 1105, 1106, 1108, 1111, 1112, 1115, 1117, 1118, 1121, 1122, 1124, 1127, 1128, 1131, 1133, 1134, 1136, 1139, 1141, 1142, 1145, 1146, 1148, 1151, 1152, 1155, 1157, 1158, 1161, 1162, 1164, 1167, 1169, 1170, 1172, 1175, 1176, 1179, 1181, 1182, 1185, 1186, 1188, 1191, 1192, 1195, 1197, 1198, 1200.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 5000000 values, from 3 to 10000000).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 2500000 | 2500000 | 2 | ||||||||
| 3 | 1775989 | 1578337 | 1645674 | 3 | |||||||
| 4 | 1250000 | 1250000 | 1250000 | 1250000 | 4 | ||||||
| 5 | 1003435 | 999715 | 997370 | 1000000 | 999480 | 5 | |||||
| 6 | 899217 | 767449 | 789895 | 876772 | 810888 | 855779 | 6 | ||||
| 7 | 714992 | 714272 | 714251 | 713772 | 714849 | 714128 | 713736 | 7 | |||
| 8 | 625000 | 625000 | 625000 | 625000 | 625000 | 625000 | 625000 | 625000 | 8 | ||
| 9 | 592015 | 526116 | 548566 | 591972 | 526103 | 548569 | 592002 | 526118 | 548539 | 9 | |
| 10 | 501910 | 498090 | 498995 | 501005 | 498475 | 501525 | 501625 | 498375 | 498995 | 501005 | 10 |
| 11 | 454612 | 454488 | 454467 | 454593 | 454513 | 454611 | 454622 | 454479 | 454478 | 454574 | 454563 |
A pictorial representation of the table above
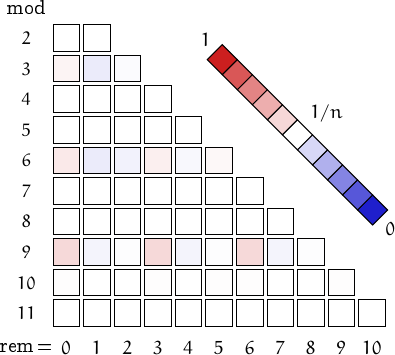
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits