The first 600 plaindromes :
1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19, 22, 23, 24, 25, 26, 27, 28, 29, 33, 34, 35, 36, 37, 38, 39, 44, 45, 46, 47, 48, 49, 55, 56, 57, 58, 59, 66, 67, 68, 69, 77, 78, 79, 88, 89, 99, 111, 112, 113, 114, 115, 116, 117, 118, 119, 122, 123, 124, 125, 126, 127, 128, 129, 133, 134, 135, 136, 137, 138, 139, 144, 145, 146, 147, 148, 149, 155, 156, 157, 158, 159, 166, 167, 168, 169, 177, 178, 179, 188, 189, 199, 222, 223, 224, 225, 226, 227, 228, 229, 233, 234, 235, 236, 237, 238, 239, 244, 245, 246, 247, 248, 249, 255, 256, 257, 258, 259, 266, 267, 268, 269, 277, 278, 279, 288, 289, 299, 333, 334, 335, 336, 337, 338, 339, 344, 345, 346, 347, 348, 349, 355, 356, 357, 358, 359, 366, 367, 368, 369, 377, 378, 379, 388, 389, 399, 444, 445, 446, 447, 448, 449, 455, 456, 457, 458, 459, 466, 467, 468, 469, 477, 478, 479, 488, 489, 499, 555, 556, 557, 558, 559, 566, 567, 568, 569, 577, 578, 579, 588, 589, 599, 666, 667, 668, 669, 677, 678, 679, 688, 689, 699, 777, 778, 779, 788, 789, 799, 888, 889, 899, 999, 1111, 1112, 1113, 1114, 1115, 1116, 1117, 1118, 1119, 1122, 1123, 1124, 1125, 1126, 1127, 1128, 1129, 1133, 1134, 1135, 1136, 1137, 1138, 1139, 1144, 1145, 1146, 1147, 1148, 1149, 1155, 1156, 1157, 1158, 1159, 1166, 1167, 1168, 1169, 1177, 1178, 1179, 1188, 1189, 1199, 1222, 1223, 1224, 1225, 1226, 1227, 1228, 1229, 1233, 1234, 1235, 1236, 1237, 1238, 1239, 1244, 1245, 1246, 1247, 1248, 1249, 1255, 1256, 1257, 1258, 1259, 1266, 1267, 1268, 1269, 1277, 1278, 1279, 1288, 1289, 1299, 1333, 1334, 1335, 1336, 1337, 1338, 1339, 1344, 1345, 1346, 1347, 1348, 1349, 1355, 1356, 1357, 1358, 1359, 1366, 1367, 1368, 1369, 1377, 1378, 1379, 1388, 1389, 1399, 1444, 1445, 1446, 1447, 1448, 1449, 1455, 1456, 1457, 1458, 1459, 1466, 1467, 1468, 1469, 1477, 1478, 1479, 1488, 1489, 1499, 1555, 1556, 1557, 1558, 1559, 1566, 1567, 1568, 1569, 1577, 1578, 1579, 1588, 1589, 1599, 1666, 1667, 1668, 1669, 1677, 1678, 1679, 1688, 1689, 1699, 1777, 1778, 1779, 1788, 1789, 1799, 1888, 1889, 1899, 1999, 2222, 2223, 2224, 2225, 2226, 2227, 2228, 2229, 2233, 2234, 2235, 2236, 2237, 2238, 2239, 2244, 2245, 2246, 2247, 2248, 2249, 2255, 2256, 2257, 2258, 2259, 2266, 2267, 2268, 2269, 2277, 2278, 2279, 2288, 2289, 2299, 2333, 2334, 2335, 2336, 2337, 2338, 2339, 2344, 2345, 2346, 2347, 2348, 2349, 2355, 2356, 2357, 2358, 2359, 2366, 2367, 2368, 2369, 2377, 2378, 2379, 2388, 2389, 2399, 2444, 2445, 2446, 2447, 2448, 2449, 2455, 2456, 2457, 2458, 2459, 2466, 2467, 2468, 2469, 2477, 2478, 2479, 2488, 2489, 2499, 2555, 2556, 2557, 2558, 2559, 2566, 2567, 2568, 2569, 2577, 2578, 2579, 2588, 2589, 2599, 2666, 2667, 2668, 2669, 2677, 2678, 2679, 2688, 2689, 2699, 2777, 2778, 2779, 2788, 2789, 2799, 2888, 2889, 2899, 2999, 3333, 3334, 3335, 3336, 3337, 3338, 3339, 3344, 3345, 3346, 3347, 3348, 3349, 3355, 3356, 3357, 3358, 3359, 3366, 3367, 3368, 3369, 3377, 3378, 3379, 3388, 3389, 3399, 3444, 3445, 3446, 3447, 3448, 3449, 3455, 3456, 3457, 3458, 3459, 3466, 3467, 3468, 3469, 3477, 3478, 3479, 3488, 3489, 3499, 3555, 3556, 3557, 3558, 3559, 3566, 3567, 3568, 3569, 3577, 3578, 3579, 3588, 3589, 3599, 3666, 3667, 3668, 3669, 3677, 3678, 3679, 3688, 3689, 3699, 3777, 3778, 3779, 3788, 3789, 3799, 3888, 3889, 3899, 3999, 4444, 4445, 4446, 4447, 4448, 4449, 4455, 4456, 4457, 4458, 4459, 4466.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 1307503 values, from 1 to 999999999999999).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 361710 | 945793 | 2 | ||||||||
| 3 | 435871 | 435816 | 435816 | 3 | |||||||
| 4 | 244750 | 322831 | 116960 | 622962 | 4 | ||||||
| 5 | 11628 | 38775 | 116400 | 320450 | 820250 | 5 | |||||
| 6 | 120580 | 315251 | 120565 | 315291 | 120565 | 315251 | 6 | ||||
| 7 | 186784 | 186791 | 186782 | 186782 | 186782 | 186791 | 186791 | 7 | |||
| 8 | 157982 | 215119 | 80580 | 233683 | 86768 | 107712 | 36380 | 389279 | 8 | ||
| 9 | 145291 | 145272 | 145272 | 145290 | 145272 | 145272 | 145290 | 145272 | 145272 | 9 | |
| 10 | 0 | 15 | 120 | 680 | 3060 | 11628 | 38760 | 116280 | 319770 | 817190 | 10 |
| 11 | 11439 | 51480 | 123552 | 205920 | 261360 | 261360 | 205920 | 123552 | 51480 | 11440 | 0 |
A pictorial representation of the table above
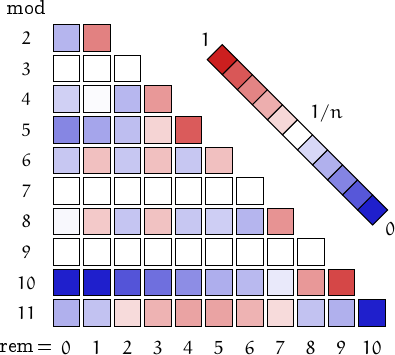
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits