The first 600 Zumkeller numbers :
6, 12, 20, 24, 28, 30, 40, 42, 48, 54, 56, 60, 66, 70, 78, 80, 84, 88, 90, 96, 102, 104, 108, 112, 114, 120, 126, 132, 138, 140, 150, 156, 160, 168, 174, 176, 180, 186, 192, 198, 204, 208, 210, 216, 220, 222, 224, 228, 234, 240, 246, 252, 258, 260, 264, 270, 272, 276, 280, 282, 294, 300, 304, 306, 308, 312, 318, 320, 330, 336, 340, 342, 348, 350, 352, 354, 360, 364, 366, 368, 372, 378, 380, 384, 390, 396, 402, 408, 414, 416, 420, 426, 432, 438, 440, 444, 448, 456, 460, 462, 464, 468, 474, 476, 480, 486, 490, 492, 496, 498, 500, 504, 510, 516, 520, 522, 528, 532, 534, 540, 544, 546, 550, 552, 558, 560, 564, 570, 572, 580, 582, 588, 594, 600, 606, 608, 612, 616, 618, 620, 624, 630, 636, 640, 642, 644, 650, 654, 660, 666, 672, 678, 680, 684, 690, 696, 700, 702, 704, 708, 714, 720, 726, 728, 732, 736, 740, 744, 750, 756, 760, 762, 768, 770, 780, 786, 792, 798, 804, 810, 812, 816, 820, 822, 828, 832, 834, 836, 840, 852, 858, 860, 864, 868, 870, 876, 880, 888, 894, 896, 906, 910, 912, 918, 920, 924, 928, 930, 936, 940, 942, 945, 948, 952, 960, 966, 972, 978, 980, 984, 990, 992, 996, 1000, 1002, 1008, 1014, 1020, 1026, 1032, 1036, 1038, 1040, 1044, 1050, 1056, 1060, 1064, 1068, 1074, 1080, 1086, 1088, 1092, 1100, 1104, 1110, 1116, 1120, 1122, 1128, 1134, 1140, 1144, 1146, 1148, 1158, 1160, 1164, 1170, 1176, 1180, 1182, 1184, 1188, 1190, 1194, 1200, 1204, 1212, 1216, 1218, 1220, 1224, 1230, 1232, 1236, 1240, 1242, 1248, 1254, 1260, 1266, 1272, 1280, 1284, 1288, 1290, 1300, 1302, 1308, 1312, 1316, 1320, 1326, 1330, 1332, 1338, 1340, 1344, 1350, 1356, 1360, 1362, 1368, 1372, 1374, 1376, 1380, 1386, 1392, 1398, 1400, 1404, 1408, 1410, 1416, 1420, 1428, 1430, 1434, 1440, 1446, 1452, 1456, 1460, 1464, 1470, 1472, 1476, 1480, 1482, 1484, 1488, 1496, 1500, 1504, 1506, 1512, 1518, 1520, 1524, 1530, 1536, 1540, 1542, 1548, 1554, 1560, 1566, 1572, 1575, 1578, 1580, 1584, 1590, 1596, 1608, 1610, 1614, 1620, 1624, 1626, 1632, 1638, 1640, 1644, 1650, 1652, 1656, 1660, 1662, 1664, 1668, 1672, 1674, 1680, 1686, 1692, 1696, 1698, 1700, 1704, 1708, 1710, 1716, 1720, 1722, 1728, 1734, 1736, 1740, 1750, 1752, 1758, 1760, 1768, 1770, 1776, 1780, 1782, 1788, 1792, 1794, 1806, 1812, 1820, 1824, 1830, 1836, 1840, 1842, 1848, 1856, 1860, 1866, 1870, 1872, 1876, 1878, 1880, 1884, 1888, 1890, 1896, 1900, 1902, 1904, 1908, 1914, 1920, 1932, 1938, 1940, 1944, 1950, 1952, 1956, 1960, 1968, 1974, 1976, 1980, 1984, 1986, 1988, 1992, 1998, 2000, 2002, 2004, 2010, 2016, 2020, 2022, 2024, 2028, 2030, 2040, 2044, 2046, 2052, 2058, 2060, 2064, 2070, 2072, 2076, 2080, 2082, 2088, 2090, 2094, 2100, 2106, 2112, 2118, 2120, 2124, 2128, 2130, 2136, 2140, 2142, 2148, 2154, 2156, 2160, 2166, 2170, 2172, 2176, 2180, 2184, 2190, 2196, 2200, 2202, 2205, 2208, 2210, 2212, 2214, 2220, 2226, 2232, 2238, 2240, 2244, 2250, 2256, 2260, 2262, 2268, 2274, 2280, 2288, 2292, 2296, 2298, 2300, 2310, 2316, 2320, 2322, 2324, 2328, 2334, 2340, 2346, 2352, 2360, 2364, 2368, 2370, 2376, 2380, 2382, 2388, 2392, 2394, 2400, 2406, 2408, 2412, 2418, 2420, 2424, 2430, 2432, 2436, 2440, 2442, 2448, 2454, 2460, 2464, 2470, 2472, 2478, 2480, 2484, 2490, 2492, 2496, 2508, 2514, 2520, 2526, 2530, 2532, 2538, 2540, 2544, 2548, 2550, 2552, 2556, 2560, 2562, 2568, 2574, 2576, 2580, 2584, 2586, 2590, 2598, 2600, 2604, 2610, 2616, 2620, 2622, 2624, 2628, 2632, 2634, 2640, 2646.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 23051 values, from 6 to 100000).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 22843 | 208 | 2 | ||||||||
| 3 | 15383 | 3836 | 3832 | 3 | |||||||
| 4 | 14597 | 104 | 8246 | 104 | 4 | ||||||
| 5 | 7371 | 3920 | 3924 | 3923 | 3913 | 5 | |||||
| 6 | 15175 | 0 | 3832 | 208 | 3836 | 0 | 6 | ||||
| 7 | 5377 | 2927 | 2918 | 2976 | 2912 | 2975 | 2966 | 7 | |||
| 8 | 8184 | 51 | 4108 | 53 | 6413 | 53 | 4138 | 51 | 8 | ||
| 9 | 4216 | 1284 | 1277 | 5583 | 1271 | 1276 | 5584 | 1281 | 1279 | 9 | |
| 10 | 7164 | 1 | 3924 | 0 | 3913 | 207 | 3919 | 0 | 3923 | 0 | 10 |
| 11 | 2873 | 2013 | 2010 | 2022 | 2023 | 2015 | 2022 | 2010 | 2016 | 2020 | 2027 |
A pictorial representation of the table above
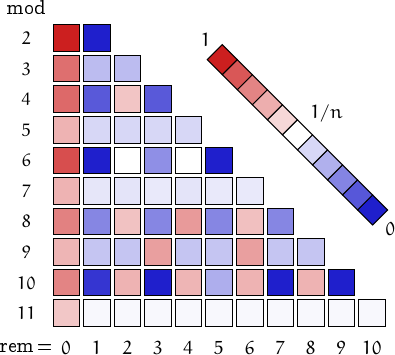
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits