The first 600 amenable numbers :
1, 5, 8, 9, 12, 13, 16, 17, 20, 21, 24, 25, 28, 29, 32, 33, 36, 37, 40, 41, 44, 45, 48, 49, 52, 53, 56, 57, 60, 61, 64, 65, 68, 69, 72, 73, 76, 77, 80, 81, 84, 85, 88, 89, 92, 93, 96, 97, 100, 101, 104, 105, 108, 109, 112, 113, 116, 117, 120, 121, 124, 125, 128, 129, 132, 133, 136, 137, 140, 141, 144, 145, 148, 149, 152, 153, 156, 157, 160, 161, 164, 165, 168, 169, 172, 173, 176, 177, 180, 181, 184, 185, 188, 189, 192, 193, 196, 197, 200, 201, 204, 205, 208, 209, 212, 213, 216, 217, 220, 221, 224, 225, 228, 229, 232, 233, 236, 237, 240, 241, 244, 245, 248, 249, 252, 253, 256, 257, 260, 261, 264, 265, 268, 269, 272, 273, 276, 277, 280, 281, 284, 285, 288, 289, 292, 293, 296, 297, 300, 301, 304, 305, 308, 309, 312, 313, 316, 317, 320, 321, 324, 325, 328, 329, 332, 333, 336, 337, 340, 341, 344, 345, 348, 349, 352, 353, 356, 357, 360, 361, 364, 365, 368, 369, 372, 373, 376, 377, 380, 381, 384, 385, 388, 389, 392, 393, 396, 397, 400, 401, 404, 405, 408, 409, 412, 413, 416, 417, 420, 421, 424, 425, 428, 429, 432, 433, 436, 437, 440, 441, 444, 445, 448, 449, 452, 453, 456, 457, 460, 461, 464, 465, 468, 469, 472, 473, 476, 477, 480, 481, 484, 485, 488, 489, 492, 493, 496, 497, 500, 501, 504, 505, 508, 509, 512, 513, 516, 517, 520, 521, 524, 525, 528, 529, 532, 533, 536, 537, 540, 541, 544, 545, 548, 549, 552, 553, 556, 557, 560, 561, 564, 565, 568, 569, 572, 573, 576, 577, 580, 581, 584, 585, 588, 589, 592, 593, 596, 597, 600, 601, 604, 605, 608, 609, 612, 613, 616, 617, 620, 621, 624, 625, 628, 629, 632, 633, 636, 637, 640, 641, 644, 645, 648, 649, 652, 653, 656, 657, 660, 661, 664, 665, 668, 669, 672, 673, 676, 677, 680, 681, 684, 685, 688, 689, 692, 693, 696, 697, 700, 701, 704, 705, 708, 709, 712, 713, 716, 717, 720, 721, 724, 725, 728, 729, 732, 733, 736, 737, 740, 741, 744, 745, 748, 749, 752, 753, 756, 757, 760, 761, 764, 765, 768, 769, 772, 773, 776, 777, 780, 781, 784, 785, 788, 789, 792, 793, 796, 797, 800, 801, 804, 805, 808, 809, 812, 813, 816, 817, 820, 821, 824, 825, 828, 829, 832, 833, 836, 837, 840, 841, 844, 845, 848, 849, 852, 853, 856, 857, 860, 861, 864, 865, 868, 869, 872, 873, 876, 877, 880, 881, 884, 885, 888, 889, 892, 893, 896, 897, 900, 901, 904, 905, 908, 909, 912, 913, 916, 917, 920, 921, 924, 925, 928, 929, 932, 933, 936, 937, 940, 941, 944, 945, 948, 949, 952, 953, 956, 957, 960, 961, 964, 965, 968, 969, 972, 973, 976, 977, 980, 981, 984, 985, 988, 989, 992, 993, 996, 997, 1000, 1001, 1004, 1005, 1008, 1009, 1012, 1013, 1016, 1017, 1020, 1021, 1024, 1025, 1028, 1029, 1032, 1033, 1036, 1037, 1040, 1041, 1044, 1045, 1048, 1049, 1052, 1053, 1056, 1057, 1060, 1061, 1064, 1065, 1068, 1069, 1072, 1073, 1076, 1077, 1080, 1081, 1084, 1085, 1088, 1089, 1092, 1093, 1096, 1097, 1100, 1101, 1104, 1105, 1108, 1109, 1112, 1113, 1116, 1117, 1120, 1121, 1124, 1125, 1128, 1129, 1132, 1133, 1136, 1137, 1140, 1141, 1144, 1145, 1148, 1149, 1152, 1153, 1156, 1157, 1160, 1161, 1164, 1165, 1168, 1169, 1172, 1173, 1176, 1177, 1180, 1181, 1184, 1185, 1188, 1189, 1192, 1193, 1196, 1197, 1200, 1201.
Distribution of the remainders when the numbers in this family are divided by n=2, 3,..., 11. (I took into account 4999999 values, from 1 to 10000000).
| n\r | 0 | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 2499999 | 2500000 | 2 | ||||||||
| 3 | 1666666 | 1666667 | 1666666 | 3 | |||||||
| 4 | 2499999 | 2500000 | 0 | 0 | 4 | ||||||
| 5 | 1000000 | 1000000 | 1000000 | 1000000 | 999999 | 5 | |||||
| 6 | 833333 | 833334 | 833333 | 833333 | 833333 | 833333 | 6 | ||||
| 7 | 714285 | 714286 | 714286 | 714286 | 714284 | 714286 | 714286 | 7 | |||
| 8 | 1250000 | 1250000 | 0 | 0 | 1249999 | 1250000 | 0 | 0 | 8 | ||
| 9 | 555555 | 555556 | 555555 | 555556 | 555555 | 555555 | 555555 | 555556 | 555556 | 9 | |
| 10 | 500000 | 500000 | 500000 | 500000 | 499999 | 500000 | 500000 | 500000 | 500000 | 500000 | 10 |
| 11 | 454544 | 454546 | 454546 | 454545 | 454544 | 454546 | 454546 | 454545 | 454545 | 454546 | 454546 |
A pictorial representation of the table above
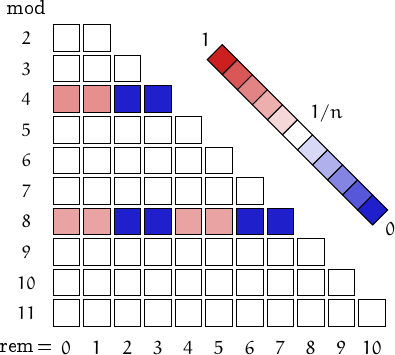
Imagine to divide the members of this family by a number n and compute the remainders. Should they be uniformly distributed, each remainder from 0 to n-1 would be obtained in about (1/n)-th of the cases. This outcome is represented by a white square. Reddish (resp. bluish) squares represent remainders which appear more (resp. less) frequently than 1/n.
e-mail: info -at- numbersaplenty.com • Privacy notice • engine limits